Cinemática del sólido rígido (G.I.T.I.)
De Laplace
(→Campo de velocidades) |
(→Campo de velocidades) |
||
| Línea 86: | Línea 86: | ||
siendo <math>\vec{v}_0</math> y <math>\vec{\omega}</math> dos vectores independientes de la posición (pero no del tiempo; son vectores uniformes, pero no constantes). Aquí <math>\vec{r}</math> es la posición respecto a un cierto punto O que tomamos como origen de coordenadas. Este es el conocido como '''Teorema de Chasles'''. | siendo <math>\vec{v}_0</math> y <math>\vec{\omega}</math> dos vectores independientes de la posición (pero no del tiempo; son vectores uniformes, pero no constantes). Aquí <math>\vec{r}</math> es la posición respecto a un cierto punto O que tomamos como origen de coordenadas. Este es el conocido como '''Teorema de Chasles'''. | ||
| + | |||
| + | Si etiquetamos la posición del origen por O y la de un punto cualquiera por P, la forma general del campo de velocidades puede escribirse como | ||
| + | |||
| + | <center><math>\vec{v}^P = \vec{v}^O + \vec{\omega}\times\overrightarrow{OP}</math></center> | ||
Antes de analizar esta solución en su forma general, consideraremos casos particulares de ella. | Antes de analizar esta solución en su forma general, consideraremos casos particulares de ella. | ||
Revisión de 09:48 28 jul 2010
Contenido |
1 Concepto de sólido rígido
Una vez descrito el sistema más sencillo, formado por una sola partícula, podemos pasar a sistemas más complejos, considerándolos formados por un agregado de partículas interactuantes.
Existen toda una serie de leyes generales y teoremas de conservación para sistemas de partículas, pero aquí nos centraremos en un agregado muy concreto, que es el modelo denominado sólido rígido.
Los sistemas macroscópicos suelen clasificarse en diferentes estados de la materia: sólidos, líquidos, gases y plasmas. De estos, los tres últimos se agrupan conjuntamente en el concepto de fluidos, por oposición a los sólidos.
La diferencia entre un fluido y un sólido es que mientras el fluido se adapta a la forma del recipiente que lo contiene, el sólido no lo hace. También se distinguen en su comportamiento cuando se ejerce una fuerza tangente a su superficie (fuerza de cizalla). Un fluido adquiere una velocidad en la dirección de la fuerza (velocidad dependiente de la viscosidad del fluido), mientras que un sólido se deforma en dicha dirección.
Todos los sólidos son deformables cuando se aplica una fuerza sobre ellos, y el grado con que lo hacen se mide por su compresiblidad. En el caso de un resorte, esta deformabilidad se mide con la constante de recuperación que aparece en la ley de Hooke.
Cuanto menor es la compresibilidad de un sólido (o mayor su constante de recuperación) más indeformable es, más fuerza es necesaria para conseguir una dilatación dada. Por ejemplo, de acuerdo con la [[ley de Hooke], el estiramiento de un resorte viene dado por
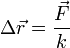
cuando 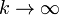 la deformación tiende a cero, sea cual sea la fuerza aplicada.
la deformación tiende a cero, sea cual sea la fuerza aplicada.
Un primer estudio de los sólidos consiste, por tanto, en hacer el modelo de sólido completamente indeformable, o sólido rígido.
2 Condición de rigidez
Matemáticamente, un sólido rígido se caracteriza por ser un sistema de partículas tal que la distancia entre cada par de partículas que lo componen permanece constante en cada momento
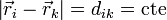
Elevando al cuadrado
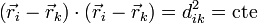
y derivando esta expresión respecto al tiempo obtenemos una condición sobre las velocidades
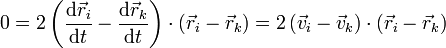
El vector
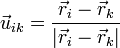
es el unitario en la dirección de la recta que une los dos puntos, por lo que la condición de rigidez implica
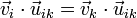
¿Cómo se interpreta este resultado? El producto escalar de un vector por un unitario es la proyección de dicho vector en la dirección del unitario. Por tanto, la condición de rigidez implica que, dadas dos partículas, i y k, la proyección de sus respectivas velocidades sobre la recta que es la une es la misma. Por ello se dice que el campo de velocidades es equiproyectivo.
El que las dos proyecciones sean iguales quiere decir que la componente de las velocidades en esa dirección es la misma; las dos partículas avanzan o retroceden a lo largo de esa línea en igual medida, manteniendo su distancia relativa.
Otra forma de verlo es considerar que 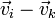 es la velocidad de la partícula i respecto a la k, y la condición de rigidez
es la velocidad de la partícula i respecto a la k, y la condición de rigidez

nos dice que la velocidad relativa de una partícula respecto a otra es siempre perpendicular a la recta que las une. Si nos montamos en una partícula del sólido lo que vemos es que todas las demás partículas ni se acercan ni se alejan, sino que giran en torno a la posición que nos encontremos.
3 Grados de libertad
El número de grados de libertad de un sistema se define como el número de coordenadas del sistema menos el número de ligaduras independientes que relacionan dichas coordenadas. En muchos casos el número de grados de libertad equivale al número de variables necesarias para describir el movimiento del sistema.
¿Cuántos grados de libertad tiene un sólido rígido? El número de coordenadas es 3N, siendo N el número de partículas. En un sólido macroscópico este número es gigantesco, pero es claro que para describir el movimiento de un sólido no necesitamos tantas variables, ya que la condición de rigidez impone muchos vínculos.
Para ver el número de variables necesarias consideramos primero una sola partícula. Para dar su posición necesitamos 3 variables, por ejemplo, sus coordenadas cartesianas.
Situamos ahora la segunda partícula. Su posición tiene 3 coordenadas, pero una de ellas es conocida, ya que sabemos que la distancia a la primera partícula es constante. La posición de la segunda partícula se encuentra sobre una esfera de radio d12 alrededor de la primera y para dar una posición sobre una esfera solo necesitamos 2 variables.
La tercera partícula se encuentra a una distancia d13 de la primera y a una distancia d23 de la segunda, por lo que solo necesitamos 1 variable para localizarla.
Para la cuarta y siguientes, la distancia a las tres primeras nos define de forma unívoca su posición, por lo que no precisamos variables adicionales.
Por tanto, el número de grados de libertad de un sólido rígido es 3+2+1 = 6. Dando seis datos, que pueden ser diferentes según las circunstancias, podemos describir de manera completa la posición y el estado de movimiento de un sólido rígido.
4 Campo de velocidades
Cuando un sólido se mueve, cada uno de sus puntos lo hará, en principio, con una velocidad diferente. Tenemos entonces que la distribución de velocidades forma un campo vectorial
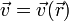
La velocidad de cada punto es un vector ligado a dicho punto y por tanto carece de sentido hablar de la “velocidad de un sólido”, como si fuera algo único. Podremos hablar de la velocidad de un punto del sólido, o en su caso, de la velocidad de su centro de masas, pero no de la velocidad del sólido como un todo.
La condición de rigidez impone limitaciones a las posibles distribuciones de velocidades. Solo aquellos movimientos que preservan las distancias entre los puntos son admisibles.
Puede demostrarse que la forma más general del campo de velocidades de un sólido es
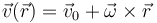
siendo  y
y  dos vectores independientes de la posición (pero no del tiempo; son vectores uniformes, pero no constantes). Aquí
dos vectores independientes de la posición (pero no del tiempo; son vectores uniformes, pero no constantes). Aquí  es la posición respecto a un cierto punto O que tomamos como origen de coordenadas. Este es el conocido como Teorema de Chasles.
es la posición respecto a un cierto punto O que tomamos como origen de coordenadas. Este es el conocido como Teorema de Chasles.
Si etiquetamos la posición del origen por O y la de un punto cualquiera por P, la forma general del campo de velocidades puede escribirse como
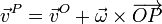
Antes de analizar esta solución en su forma general, consideraremos casos particulares de ella.
5 Movimiento de traslación
Supongamos, en primer lugar, que
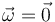
En este caso, el campo de velocidades se reduce a
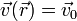
esto es, todos los puntos del sólido se mueven con la misma velocidad instantánea. Cuando esto ocurre se dice que el sólido experimenta un movimiento de traslación.
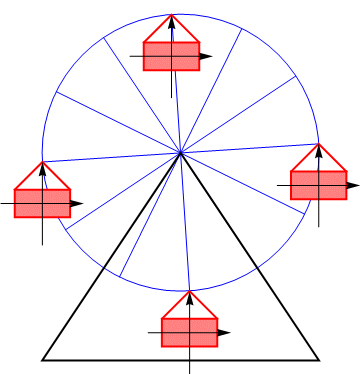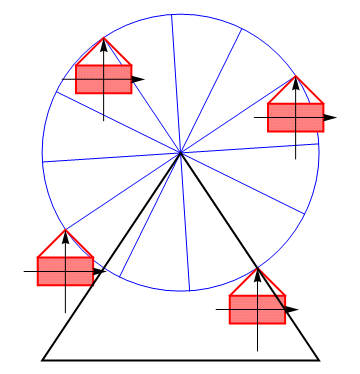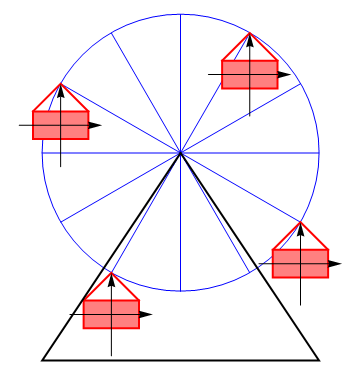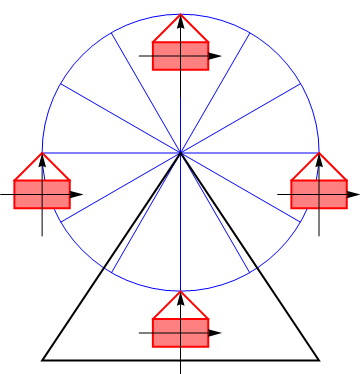
Si fijamos un sistema de ejes al sólido, estos mantienen su orientación en un movimiento de traslación.
Hay que insistir en que hablamos de velocidades instantáneas y del movimiento relativo de los diferentes puntos del sólido. Un movimiento de traslación NO significa que el sólido se mueve en línea recta, o a velocidad constante.
Por ejemplo, consideremos el movimiento de un vagón de una noria. Puesto que éste no se da la vuelta, sino que conserva en todo momento su orientación vertical, llegamos a la conclusión de que el sólido experimenta un movimiento de traslación. Cada uno de sus puntos se mueve en cada instante con la misma velocidad que el resto de los puntos, aunque esta velocidad sea cambiante.
5.1 Traslación permanente
En el caso más restrictivo
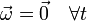
implica un movimiento de traslación permanente: los ejes ligados al sólido conservan su orientación en cada instante y el movimiento de cada uno de los puntos del sólido reproduce exactamente el de cualquier otro de ellos.
Este movimiento no tiene por qué ser ni rectilíneo ni uniforme. Como en el caso de la noria, es posible que cada uno de los puntos escriba una circunferencia en torno a un centro (siendo este centro diferente para cada punto del sólido).
6 Movimiento de rotación
Supongamos ahora que
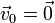
de forma que la velocidad instantánea de cada punto se reduce a
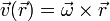
Esta forma del campo de velocidades posee una serie de propiedades que lo identifican como movimiento de rotación:
- Existe una línea recta (eje instantáneo de rotación, EIR) cuyos puntos poseen velocidad nula
- El EIR pasa por el origen de coordenadas y tiene la dirección dada por
 .
.
- La velocidad de que cualquier otro punto es perpendicular al eje de rotación.
- Todos los puntos a la misma distancia del eje poseen la misma celeridad.
- La celeridad de cada punto es proporcional a su distancia al eje.
- El sentido de las velocidades cumple la regla de la mano derecha respecto al vector
 .
.
7 Movimiento helicoidal
Consideremos ahora el caso más general en que ni  ni
ni  son nulos, pero sí paralelos:
son nulos, pero sí paralelos:
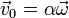
Este campo de velocidades posee una serie de propiedades:
- Existe una recta, paralela a la velocidad angular, tal que la velocidad de sus puntos posee módulo mínimo y dirección la de la propia recta (eje instantáneo de rotación y mínimo deslizamiento, EIRMD).
- El EIRMD pasa por el origen de coordenadas y tiene la dirección de la velocidad angular.
- Todos los puntos situados a la misma distancia de este eje poseen la misma celeridad.
- La proyección de la velocidad de cada punto sobre la velocidad angular es la misma para todos los puntos.
- La velocidad de todos los puntos situados a la misma distancia forma el mismo ángulo con la velocidad angular.
- El sentido de la velocidad cumple la regla de la mano derecha respecto a la velocidad angular.