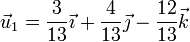1.12. Ejemplo de construcción de una base
De Laplace
(Diferencias entre revisiones)
(→Primer vector) |
(→Primer vector) |
||
| Línea 20: | Línea 20: | ||
por lo que | por lo que | ||
| - | <center><math>\vec{ | + | <center><math>\vec{u}_1 = \frac{3}{13}\vec{\imath}+\frac{4}{13}\vec{\jmath}-\frac{12}{13}\vec{k}</math></center> |
==Segundo vector== | ==Segundo vector== | ||
==Tercer vector== | ==Tercer vector== | ||
[[Categoría:Problemas de vectores libres (G.I.T.I.)]] | [[Categoría:Problemas de vectores libres (G.I.T.I.)]] | ||
Revisión de 16:03 21 jul 2010
Contenido |
1 Enunciado
Dados los vectores
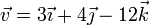
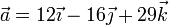
Construya una base ortonormal dextrógira, tal que
- El primer vector vaya en la dirección de
- El segundo esté contenido en el plano definido por y
- El tercero sea perpendicular a los dos anteriores, y orientado según la regla de la mano derecha.
2 Primer vector
Obtenemos el primer vector normalizando el vector , esto es, hallando el unitario en su dirección y sentido, lo que se consigue dividiendo este vector por su módulo
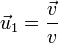
Hallamos el módulo de
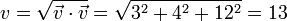
por lo que
