Problemas de vectores libres (G.I.T.I.)
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Ejemplo de construcción de una base== Dados los vectores <center><math>\vec{v}=3\vec{\imath}+4\vec{\jmath}-12\vec{k}</math>{{qquad}}{{qquad}}<math>\vec{a}=12\vec{\imath}…') |
(→Ejemplo de construcción de una base) |
||
| Línea 2: | Línea 2: | ||
Dados los vectores | Dados los vectores | ||
| - | <center><math>\vec{v}=3\vec{\imath}+4\vec{\jmath}-12\vec{k}</math>{{qquad}}{{qquad}}<math>\vec{a}=12\vec{\imath}-16\vec{\jmath}+29\vec{ | + | <center><math>\vec{v}=3\vec{\imath}+4\vec{\jmath}-12\vec{k}</math>{{qquad}}{{qquad}}<math>\vec{a}=12\vec{\imath}-16\vec{\jmath}+29\vec{k}</math></center> |
Construya una base ortonormal dextrógira, tal que | Construya una base ortonormal dextrógira, tal que | ||
| Línea 11: | Línea 11: | ||
[[Categoría:Problemas de vectores libres (G.I.T.I)|0]] | [[Categoría:Problemas de vectores libres (G.I.T.I)|0]] | ||
| - | [[Categoría:Vectores libres (G.I.T.I | + | [[Categoría:Vectores libres (G.I.T.I)]] |
Revisión de 12:54 21 jul 2010
Ejemplo de construcción de una base
Dados los vectores
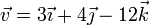
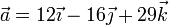
Construya una base ortonormal dextrógira, tal que
- El primer vector vaya en la dirección de

- El segundo esté contenido en el plano definido por \vec{v} y \vec{a}
- El tercero sea perpendicular a los dos anteriores, y orientado según la regla de la mano derecha.





