Vectores libres
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Magnitudes escalares y vectoriales== Una '''magnitud física''' es cualquier propiedad física susceptible de ser medida. Ejemplos: el tiempo (<math>t</math>), la velocidad (<…') |
(→Magnitudes escalares y vectoriales) |
||
| Línea 6: | Línea 6: | ||
;Magnitudes escalares: son aquéllas que quedan completamente determinadas mediante el conocimiento de su valor expresado mediante una cantidad (un número real) seguida de una unidad (a excepción de las adimensionales). Ejemplos: el tiempo (<math>t</math>), la masa | ;Magnitudes escalares: son aquéllas que quedan completamente determinadas mediante el conocimiento de su valor expresado mediante una cantidad (un número real) seguida de una unidad (a excepción de las adimensionales). Ejemplos: el tiempo (<math>t</math>), la masa | ||
(<math>m</math>), la temperatura (<math>T</math>), la carga eléctrica (<math>q</math>), el coeficiente de rozamiento (<math>\mu</math>). | (<math>m</math>), la temperatura (<math>T</math>), la carga eléctrica (<math>q</math>), el coeficiente de rozamiento (<math>\mu</math>). | ||
| - | ;Magnitudes vectoriales: son aquéllas que no quedan completamente determinadas por su valor (cantidad y unidad), sino que requieren además el conocimiento de la dirección y el sentido de su actuación, e incluso en algunos casos el conocimiento de su recta soporte o de su punto de aplicación. Ejemplos: la velocidad (<math>\vec{v}</math>), la aceleración (<math>\vec{a}</math>), la fuerza (<math>\vec{F}</math>), el | + | ;Magnitudes vectoriales: son aquéllas que no quedan completamente determinadas por su valor (cantidad y unidad), sino que requieren además el conocimiento de la dirección y el sentido de su actuación, e incluso en algunos casos el conocimiento de su recta soporte o de su punto de aplicación. Ejemplos: la velocidad (<math>\vec{v}</math>), la aceleración (<math>\vec{a}</math>), la fuerza (<math>\vec{F}</math>), el campo eléctrico (<math>\vec{E}</math>). |
| - | campo eléctrico (<math>\vec{E}</math>). | + | |
;Magnitudes tensoriales: generalizan el concepto de magnitud vectorial. Mientras las vectoriales pueden ser representadas por una matriz 3×1, las tensoriales requieren matrices 3×3 o incluso entes de mayores dimenriones. | ;Magnitudes tensoriales: generalizan el concepto de magnitud vectorial. Mientras las vectoriales pueden ser representadas por una matriz 3×1, las tensoriales requieren matrices 3×3 o incluso entes de mayores dimenriones. | ||
Revisión de 10:08 19 jul 2010
Magnitudes escalares y vectoriales
Una magnitud física es cualquier propiedad física susceptible de ser medida. Ejemplos: el tiempo (t), la velocidad
(
), la masa (m), la temperatura (T), el campo eléctrico (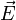
).
Las magnitudes físicas se pueden clasificar en:
- Magnitudes escalares
- son aquéllas que quedan completamente determinadas mediante el conocimiento de su valor expresado mediante una cantidad (un número real) seguida de una unidad (a excepción de las adimensionales). Ejemplos: el tiempo (t), la masa
(m), la temperatura (T), la carga eléctrica (q), el coeficiente de rozamiento (μ).
- Magnitudes vectoriales
- son aquéllas que no quedan completamente determinadas por su valor (cantidad y unidad), sino que requieren además el conocimiento de la dirección y el sentido de su actuación, e incluso en algunos casos el conocimiento de su recta soporte o de su punto de aplicación. Ejemplos: la velocidad (), la aceleración (
), la fuerza (
), el campo eléctrico ().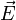
- Magnitudes tensoriales
- generalizan el concepto de magnitud vectorial. Mientras las vectoriales pueden ser representadas por una matriz 3×1, las tensoriales requieren matrices 3×3 o incluso entes de mayores dimenriones.
