Teorema de Poynting en un cable coaxial
De Laplace
(→Enunciado) |
(→Campos eléctrico y magnético) |
||
| Línea 10: | Línea 10: | ||
==Solución== | ==Solución== | ||
===Campos eléctrico y magnético=== | ===Campos eléctrico y magnético=== | ||
| + | Dado que la situación es estática, pues ni <math>V_0</math> ni <math>I_0</math> dependen del tiempo, los problemas eléctrico y magnético están desacoplados. Por tanto pueden resolverse independientemente. | ||
| + | |||
====Campo eléctrico==== | ====Campo eléctrico==== | ||
| + | Dada la simetría cilíndrica del problema, escogeremos estas coordenadas, con el eje $z$ coincidente con el eje central del cable. Al ser el campo magnético estacionario el campo eléctrico es irrotacional en todo el espacio, $\nabla\times\mathbf{E}=0$. Resolveremos entonces la ecuación del potencial electrostático en cada región definida por los conductores. Este apartado se reduce al estudio de un condensador coaxial. | ||
| + | |||
| + | Por simetría el potencial en cada región sólo puede depender de la coordenada radial cilíndrica $\rho$. | ||
| + | |||
| + | * <math>\rho<a</math>: El núcleo de cable está sometido a un potencial $V_0$. Al ser un conductor perfecto es equipotencial, con lo que $\phi=V_0$ en todos sus puntos y, por tanto, $\mathbf{E}(\rho<a)=0$. | ||
| + | |||
| + | * <math>a<\rho<b</math>: En esta región no hay densidad volumétrica de carga. El núcleo está a un potencial $V_0$ y la carcasa exterior a tierra. Entonces el problema de potencial queda | ||
| + | |||
| + | <center><math>\nabla^2\phi = 0 \quad\Rightarrow\quad \frac{1}{\rho}\frac{\mathrm{d}\ }{\mathrm{d}\rho}\left( | ||
| + | \rho\frac{\mathrm{d}\phi }{\mathrm{d}\rho}\right) = 0 | ||
| + | \quad\Rightarrow\quad \phi = A\ln\rho + B</math></center> | ||
| + | |||
| + | con las condiciones | ||
| + | |||
| + | <center><math>\phi(\rho = a) = V_0\qquad \phi(\rho = b) = 0</math></center> | ||
| + | |||
| + | siendo la solución final | ||
| + | |||
| + | <center><math>\phi(\rho) = -\frac{V_0}{\ln(b/a)}\ln(\rho/b)</math></center> | ||
| + | |||
| + | El campo eléctrico en esta región es | ||
| + | |||
| + | <center><math>\mathbf{E}(a<\rho<b) = -\nabla\phi = -\dtot{\phi}{\rho}\mathbf{u}_{\rho} = \dfrac{V_0}{\ln(b/a)}\dfrac{1}{\rho}\mathbf{u}_{\rho}</math></center> | ||
| + | |||
| + | *<math>\rho>b</math>: Aquí tampoco hay carga en volumen, por lo que el potencial es armónico. Las condiciones de contorno son homogéneas, pues <math>\phi(\rho=b) = 0</math> y <math>\phi(\rho\to\infty)=0</math>. Entonces el potencial es nulo y por tanto el campo eléctrico también. | ||
| + | |||
| + | Recapitulando, el campo eléctrico en todos los puntos del espacio es | ||
| + | |||
| + | <center><math>\mathbf{E}=\begin{cases}{\mathbf{0} & \rho<a\\ & \\ | ||
| + | \displaystyle\frac{V_0}{\ln(b/a)}\frac{1}{\rho}\mathbf{u}_{\rho} & a<\rho<b \\ & \\ | ||
| + | 0 & \rho>b\end{cases}</math></center> | ||
| + | |||
| + | Es discontinuo en <math>\rho=a</math> y <math>\rho=b</math>, debido a las densidades superficiales de carga que aparecen en la superficie del núcleo y en la carcasa exterior. | ||
| + | |||
====Campo magnético==== | ====Campo magnético==== | ||
Revisión de 17:24 2 jun 2008
Contenido |
1 Enunciado
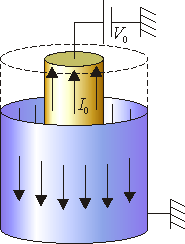
Un cable coaxial ideal está formado por un cilindro interior, de radio a, perfectamente conductor, y una superficie cilíndrica exterior, de radio b, también perfectamente conductora. Los cilindros se extienden indefinidamente a lo largo de su eje.El cilindro interior se encuentra a una tensión V0, mientras que la superficie exterior se encuentra a tierra. Simultáneamente, por la superficie del núcleo fluye una corriente I0 en la dirección del eje, distribuida uniformemente. Esta corriente retorna por la superficie exterior, con lo que hay distribuida uniformemente una corriente − I0.
- Halle los campos eléctrico y magnético en todos los puntos del espacio.
- Calcule las densidades de energía eléctrica y magnética por unidad de volumen, así como la energía total almacenada en una porción de longitud h del cable coaxial.
- Determine el vector de Poynting en el espacio entre los cilindros. ¿En qué dirección fluye la energía? Halle el flujo de energía a través de una sección del cable coaxial.
2 Solución
2.1 Campos eléctrico y magnético
Dado que la situación es estática, pues ni V0 ni I0 dependen del tiempo, los problemas eléctrico y magnético están desacoplados. Por tanto pueden resolverse independientemente.
2.1.1 Campo eléctrico
Dada la simetría cilíndrica del problema, escogeremos estas coordenadas, con el eje $z$ coincidente con el eje central del cable. Al ser el campo magnético estacionario el campo eléctrico es irrotacional en todo el espacio, $\nabla\times\mathbf{E}=0$. Resolveremos entonces la ecuación del potencial electrostático en cada región definida por los conductores. Este apartado se reduce al estudio de un condensador coaxial.
Por simetría el potencial en cada región sólo puede depender de la coordenada radial cilíndrica $\rho$.
- ρ < a: El núcleo de cable está sometido a un potencial $V_0$. Al ser un conductor perfecto es equipotencial, con lo que $\phi=V_0$ en todos sus puntos y, por tanto, $\mathbf{E}(\rho<a)=0$.
- a < ρ < b: En esta región no hay densidad volumétrica de carga. El núcleo está a un potencial $V_0$ y la carcasa exterior a tierra. Entonces el problema de potencial queda
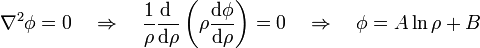
con las condiciones

siendo la solución final

El campo eléctrico en esta región es
- ρ > b: Aquí tampoco hay carga en volumen, por lo que el potencial es armónico. Las condiciones de contorno son homogéneas, pues φ(ρ = b) = 0 y
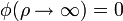 . Entonces el potencial es nulo y por tanto el campo eléctrico también.
. Entonces el potencial es nulo y por tanto el campo eléctrico también.
Recapitulando, el campo eléctrico en todos los puntos del espacio es
Es discontinuo en ρ = a y ρ = b, debido a las densidades superficiales de carga que aparecen en la superficie del núcleo y en la carcasa exterior.