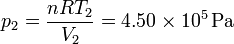Caso práctico de ciclo de Stirling
De Laplace
(→Trabajo, calor y energía) |
(→Presiones, volúmenes y temperaturas) |
||
| Línea 20: | Línea 20: | ||
El volumen que ocupa el gas lo obtenemos sabiendo el número de moles de gas: | El volumen que ocupa el gas lo obtenemos sabiendo el número de moles de gas: | ||
| - | <center><math>V_1 = \frac{n R T_1}{p_1}=\frac{100\times 8.31\times 300}{ | + | <center><math>V_1 = \frac{n R T_1}{p_1}=\frac{100\times 8.31\times 300}{1.50\times 10^5}\,\mathrm{m}^3 = 1.66\,\mathrm{m}^3</math></center> |
Nótese que, dado que estamos trabajando en el sistema internacional, el volumen resultante aparece en m³. | Nótese que, dado que estamos trabajando en el sistema internacional, el volumen resultante aparece en m³. | ||
| Línea 31: | Línea 31: | ||
Obtenemos el volumen de la misma manera | Obtenemos el volumen de la misma manera | ||
| - | <center><math>V_3 = \frac{n R T_3}{p_3}=\frac{100\times 8.31\times 2000}{3\ | + | <center><math>V_3 = \frac{n R T_3}{p_3}=\frac{100\times 8.31\times 2000}{3.00\times 10^6}\,\mathrm{m}^3 = 0.554\,\mathrm{m}^3</math></center> |
| + | |||
| + | ====Estado 2==== | ||
| + | Para el final de la compresión isoterma, observamos que su temperatura es la misma que la del estado 1 y su volumen el mismo del estado 3 | ||
| + | |||
| + | <center><math>V_2 = V_3 = 0.554\,\mathrm{m}^3</math>{{qquad}}{{qquad}}<math>T_2 = T_f = 300\,\mathrm{K}</math></center> | ||
| + | |||
| + | Con estos dos datos obtenemos la presión | ||
| + | |||
| + | <center><math>p_2 = \frac{n R T_2}{V_2}= 4.50\times 10^5\,\mathrm{Pa}</math></center> | ||
===Trabajo, calor y energía=== | ===Trabajo, calor y energía=== | ||
Revisión de 16:11 9 jul 2010
Contenido |
1 Enunciado
100 moles de gas ideal diátomico sufre un ciclo de Stirling internamente reversible, representado en la figura. El ciclo se compone de dos isotermas y dos isócoras. Las temperaturas de trabajo son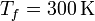 
y 
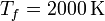, mientras que las presiones extremas son 
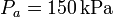y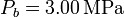 
.
- En cada uno de los procesos, calcula la variación de energía interna, el trabajo realizado y el calor absorbido por el gas. Calcula el rendimiento del ciclo.
- Calcula la variación de entropía en cada proceso del ciclo y la variación neta en el ciclo completo.
- Compara el rendimiento del ciclo con el de una máquina de Carnot reversible que trabaje entre las mismas temperaturas.
- Imagina y describe un experimento que te permita recorrer el ciclo.
Dato: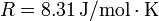 
2 Intercambios energéticos
2.1 Presiones, volúmenes y temperaturas
Antes de calcular el trabajo y el calor en cada proceso, vamos a hallar la presión, la temperatura y el volumen en cada uno de los vértices del ciclo, ya que necesitaremos estos datos más adelante.
2.1.1 Estado inicial 1
Para el estado “1” conocemos tanto su presión y su temperatura
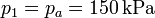
El volumen que ocupa el gas lo obtenemos sabiendo el número de moles de gas:
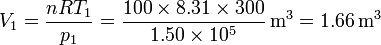
Nótese que, dado que estamos trabajando en el sistema internacional, el volumen resultante aparece en m³.
2.1.2 Estado 3
Para el estado 3 también conocemos tanto la presión como la temperatura
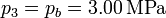
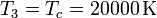
Obtenemos el volumen de la misma manera
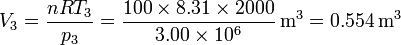
2.1.3 Estado 2
Para el final de la compresión isoterma, observamos que su temperatura es la misma que la del estado 1 y su volumen el mismo del estado 3
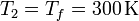
Con estos dos datos obtenemos la presión
