Teorema de Poynting para un condensador
De Laplace
(Diferencias entre revisiones)
(→Enunciado) |
|||
| Línea 8: | Línea 8: | ||
==Solución== | ==Solución== | ||
| + | ===Campo eléctrico y corriente=== | ||
| + | ===Campo magnético=== | ||
| + | ===Vector de Poynting y flujo de energía=== | ||
| + | ===Balance energético=== | ||
[[Categoría:Problemas de ecuaciones de Maxwell]] | [[Categoría:Problemas de ecuaciones de Maxwell]] | ||
Revisión de 11:33 2 jun 2008
Contenido |
1 Enunciado
El espacio entre dos placas circulares perfectamente conductoras, planas y paralelas, se encuentra lleno de un material óhmico, de permitividad 
, conductividad σ, y permeabilidad magnética μ0. El radio de las placas es b, y la distancia entre ellas es a (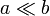
). La placa superior está permanentemente a tierra, mientras que el centro de la inferior se encuentra a una tensión V(t).
- Despreciando los efectos de borde y la inducción electromagnética, halle el campo eléctrico entre las placas y la corriente total que fluye entre ellas.
- Calcule el campo magnético entre las placas, teniendo en cuenta que en el eje
.
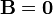- Halle el vector de Poynting en el espacio entre las placas, así como su flujo a través de una superficie cilíndrica de radio b y altura a, concéntrica con el sistema.
- ¿A qué equivale este flujo del vector de Poynting? ¿En qué caso es nulo? ¿Qué representa este caso?
