Espiral logarítmica

De Laplace

(Diferencias entre revisiones)

Revisión de 14:08 25 jun 2010

Contenido

1 Enunciado
2 Ley horaria
3 Tiempo en llegar al origen
4 Aceleración
5 Centros de curvatura

1 Enunciado

Una partícula recorre la espiral logarítmica de ecuación

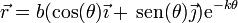
$\vec{r} = b (\cos(\theta)\vec{\imath}+\,\mathrm{sen}(\theta)\vec{\jmath})\mathrm{e}^{-k\theta}$

donde $b$ y $k$ son constantes. El movimiento es uniforme a lo largo de la curva, con celeridad constante $v 0$ . En el instante inicial la partícula se encuentra en $θ = 0$

Determine la ley horaria $θ = θ(t)$ .
Calcule el tiempo que tarda en llegar a 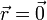$\vec{r}=\vec{0}$ . ¿Cuántas vueltas da para ello?
Halle el vector aceleración y sus componentes intrínsecas en cada punto de la trayectoria.
Determine la posición de los centros de curvatura de este movimiento.

2 Ley horaria

Para hallar la ley horaria $θ = θ(t)$ aplicamos que el movimiento es uniforme y por tanto

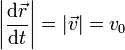
$\left|\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}\right| = |\vec{v}| = v_0$

Sin embargo, lo que se nos da es la trayectoria como función de la coordenada $θ$ y la velocidad no es la derivada de la posición respecto a $θ$ , sino respecto al tiempo. Para relacionar las dos cosas aplicamos la regla de la cadena

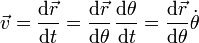
$\vec{v}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}\theta}\,\frac{\mathrm{d}\theta}{\mathrm{d}t}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}\theta}\dot{\theta}$

Aquí 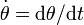$\dot{\theta} =\mathrm{d}\theta/\mathrm{d}t$ es una función que debemos determinar.

Tomando módulos

$v_0= \left|\vec{v}\right|= \left|\frac{\mathrm{d}\vec{r}}{\mathrm{d}\theta}\right|\dot{\theta}$

Derivando en la ecuación de la trayectoria

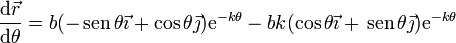
$\displaystyle\frac{\mathrm{d}\vec{r}}{\mathrm{d}\theta} = b(-\,\mathrm{sen}\,\theta\vec{\imath}+\cos\theta\vec{\jmath})\mathrm{e}^{-k\theta}-bk(\cos\theta\vec{\imath}+\,\mathrm{sen}\,\theta\vec{\jmath})\mathrm{e}^{-k\theta}$

Podemos simplificar esta expresión definiendo dos vectores unitarios

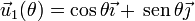
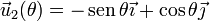
$\vec{u}_1(\theta) = \cos\theta\vec{\imath}+\,\mathrm{sen}\,\theta\vec{\jmath}$ $\vec{u}_2(\theta) = -\,\mathrm{sen}\,\theta\vec{\imath}+\cos\theta\vec{\jmath}$

Estos vectores verifican que son unitarios y ortogonales

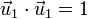
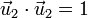
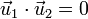
$\vec{u}_1\cdot\vec{u}_1=1$ $\vec{u}_2\cdot\vec{u}_2=1$ $\vec{u}_1\cdot\vec{u}_2=0$

y tienen por derivadas

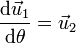
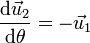
$\frac{\mathrm{d}\vec{u}_1}{\mathrm{d}\theta}=\vec{u}_2$ $\frac{\mathrm{d}\vec{u}_2}{\mathrm{d}\theta}=-\vec{u}_1$

Con ayuda de estos vectores, la posición se expresa

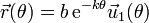
$\vec{r}(\theta)=b\,\mathrm{e}^{-k\theta}\vec{u}_1(\theta)$

y la derivada respecto al ángulo $θ$

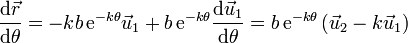
$\frac{\mathrm{d}\vec{r}}{\mathrm{d}\theta}=-k b\,\mathrm{e}^{-k\theta}\vec{u}_1+b\,\mathrm{e}^{-k\theta}\frac{\mathrm{d}\vec{u}_1}{\mathrm{d}\theta}=b\,\mathrm{e}^{-k\theta}\left(\vec{u}_2-k\vec{u}_1\right)$

que es la expresión que ya teníamos, pero más concisa.

Imponiendo ahora que la celeridad es $v 0$ queda

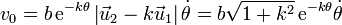
$v_0 = b\,\mathrm{e}^{-k\theta}\left|\vec{u}_2-k\vec{u}_1\right|\dot{\theta}=b\sqrt{1+k^2}\,\mathrm{e}^{-k\theta}\dot{\theta}$

Para integrar esta ecuación separamos los diferenciales

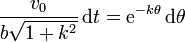
$\frac{v_0}{b\sqrt{1+k^2}}\,\mathrm{d}t = \mathrm{e}^{-k\theta}\,\mathrm{d}\theta$

e integramos, teniendo en cuenta que para $t = 0$ , $θ = 0$

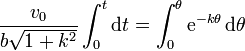
$\frac{v_0}{b\sqrt{1+k^2}}\int_0^t\mathrm{d}t = \int_0^\theta \mathrm{e}^{-k\theta}\,\mathrm{d}\theta$

lo que nos da

No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \frac{v_0 t}{b\sqrt{1+k^2}} = \left.\left(-\frac{\mathrm{e}^{-k\theta}{k}\right)\right|_0^\theta = \frac{1-\mathrm{e}^{-k\theta}}{k}

Despejando de aquí

$<math>\theta = -\frac{1}{k}\ln\left(1-\frac{v_0k}{b\sqrt{1+k^2}}t\right)$

3 Tiempo en llegar al origen

4 Aceleración

5 Centros de curvatura

@@ Línea 67: / Línea 67: @@
 lo que nos da
-<center><math>\frac{v_0 t}{b\sqrt{1+k^2}} = \left.\left(-\frac{\mathrm{e}^{-k\theta}{k\right)\right|_0^\theta = \frac{1-\mathrm{e}^{-k\theta}}{k}</math></center>
+<center><math>\frac{v_0 t}{b\sqrt{1+k^2}} = \left.\left(-\frac{\mathrm{e}^{-k\theta}{k}\right)\right|_0^\theta = \frac{1-\mathrm{e}^{-k\theta}}{k}</math></center>
 Despejando de aquí

Espiral logarítmica

De Laplace

Revisión de 14:08 25 jun 2010

Contenido

1 Enunciado

2 Ley horaria

3 Tiempo en llegar al origen

4 Aceleración

5 Centros de curvatura

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES