Entrar Página Discusión Historial Go to the site toolbox

Cinemática del tiro parabólico

De Laplace

(Diferencias entre revisiones)
(→Componentes intrínsecas de la aceleración)
(→Aceleración normal)
Línea 124: Línea 124:
;Instante inicial:
;Instante inicial:
-
<center><math>a_{n1}=g\cos\alpha</math></center>
+
<center><math>a_{n1}=g\cos\alpha\,</math></center>
;Punto de máxima altura:
;Punto de máxima altura:
-
<center><math>a_{n2}=g</math></center>
+
<center><math>a_{n2}=g\,</math></center>
;Punto de impacto
;Punto de impacto
-
<center><math>a_{n3}=g\cos\alpha</math></center>
+
<center><math>a_{n3}=g\cos\alpha\,</math></center>
===Vector normal===
===Vector normal===

Revisión de 21:41 21 jun 2010

Contenido

1 Enunciado

Supóngase el movimiento de un proyectil, dado en coordenadas cartesianas por

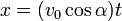
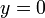
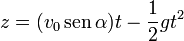
x=(v_0\cos\alpha)t\,        y=0\,        z=(v_0\,\mathrm{sen}\,\alpha)t-\frac{1}{2}gt^2
  1. Determine el vector de posición, la velocidad y la aceleración en cada instante.
  2. Calcule la celeridad y el vector tangente en el instante inicial, en el instante en que se encuentra a mayor altura y en el momento en que vuelve a impactar con el suelo.
  3. Halle la aceleración tangencial y la aceleración normal, así como el vector unitario normal en los tres instantes anteriores.
  4. Calcule el radio de curvatura y el centro de curvatura en los mismos tres instantes.

2 Posición, velocidad y aceleración

2.1 Vector de posición

Empleando la base cartesiana

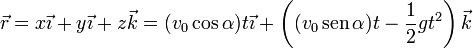
\vec{r}=x\vec{\imath}+y\vec{\imath}+z\vec{k}=(v_0\cos\alpha)t\vec{\imath}+\left((v_0\,\mathrm{sen}\,\alpha)t-\frac{1}{2}gt^2\right)\vec{k}

2.2 Velocidad

Derivando el vector de posición respecto al tiempo

\vec{v}=\dot{\vec{r}}=(v_0\cos\alpha)\vec{\imath}+\left(v_0\,\mathrm{sen}\,\alpha-gt\right)\vec{k}

2.3 Aceleración

Derivamos la velocidad instantánea respecto al tiempo

\vec{a}=\dot{\vec{v}}=-g\vec{k}

La aceleración en este movimiento es constante e igual a la de la gravedad, como corresponde a que la partícula se encuentra en caída libre.

3 Celeridad y vector tangente

Los tres instantes en que debemos calcular las diferentes magnitudes son:

Instante inicial
La partícula despega en t1 = 0.
Punto de máxima altura
La máxima altura se alcanza cuando z tiene un máximo, esto es, cuando la componente z de la velocidad es nula
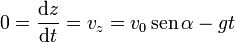
0 = \frac{\mathrm{d}z}{\mathrm{d}t}=v_z = v_0\,\mathrm{sen}\,\alpha-gt   \Rightarrow    t_2 = \frac{v_0\,\mathrm{sen}\,\alpha}{g}
Punto de impacto
el proyectil choca de nuevo con el suelo cuando z = 0, lo que ocurre en el instante
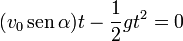
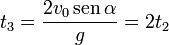
(v_0\,\mathrm{sen}\,\alpha)t-\frac{1}{2}gt^2=0   \Rightarrow    t_3=\frac{2v_0\,\mathrm{sen}\,\alpha}{g} = 2t_2

El tiempo que tarda en impactar es el doble del que tarda en llegar al punto más alto, como corresponde a que el movimiento es simétrico respecto a este punto, que es el vértice de la parábola.

La posiciones, velocidades y aceleraciones, en estos tres instantes las hallamos sustituyendo en las ecuaciones anteriores

Instante inicial
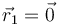
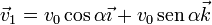
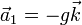
\vec{r}_1=\vec{0}        \vec{v}_1=v_0\cos\alpha\vec{\imath}+v_0\,\mathrm{sen}\,\alpha\vec{k}        \vec{a}_1=-g\vec{k}
Punto de máxima altura
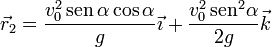
\vec{r}_2=\frac{v_0^2\,\mathrm{sen}\,\alpha\cos\alpha}{g}\vec{\imath}+\frac{v_0^2\,\mathrm{sen}^2\alpha}{2g}\vec{k}        \vec{v}_2=v_0\cos\alpha\vec{\imath}        \vec{a}_2=-g\vec{k}
Punto de impacto
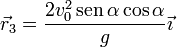
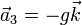
\vec{r}_3=\frac{2v_0^2\,\mathrm{sen}\,\alpha\cos\alpha}{g}\vec{\imath}        \vec{v}_3=v_0\cos\alpha\vec{\imath}-v_0\,\mathrm{sen}\,\alpha\vec{k}        \vec{a}_3=-g\vec{k}

3.1 Celeridad

la celeridad es el módulo de la velocidad. Para los tres instantes anteriores vale

Instante inicial
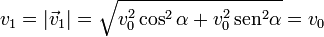
v_1 = |\vec{v}_1| = \sqrt{v_0^2\cos^2\alpha+v_0^2\,\mathrm{sen}^2\alpha}=v_0
Punto de máxima altura
v_2 = v_0\cos\alpha\,
Punto de impacto
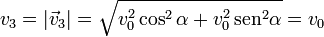
v_3 = |\vec{v}_3| = \sqrt{v_0^2\cos^2\alpha+v_0^2\,\mathrm{sen}^2\alpha}=v_0

3.2 Vector tangente

Obtenemos el vector tangente en cada uno de los instantes dividiendo la velocidad por su módulo

Instante inicial
\vec{T}_1 = \frac{\vec{v}_1}{v_1}=\cos\alpha\vec{\imath}+\,\mathrm{sen}\,\alpha\vec{k}
Punto de máxima altura
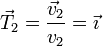
\vec{T}_2 = \frac{\vec{v}_2}{v_2}=\vec{\imath}
Punto de impacto
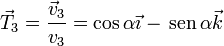
\vec{T}_3 = \frac{\vec{v}_3}{v_3}=\cos\alpha\vec{\imath}-\,\mathrm{sen}\,\alpha\vec{k}

4 Componentes intrínsecas de la aceleración

4.1 Aceleración tangencial

Obtenemos la componente tangencial de la aceleración proyectando sobre el vector tangente

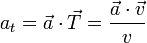
a_t = \vec{a}\cdot\vec{T}=\frac{\vec{a}\cdot\vec{v}}{v}

Para los tres instantes señalados es

Instante inicial
a_{t1}=-g\,\mathrm{sen}\,\alpha
Punto de máxima altura
a_{t2}=0\,
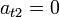
Punto de impacto
a_{t3}=g\,\mathrm{sen}\,\alpha

Vemos que, aunque la aceleración es constante, la aceleración tangencial no lo es. En el instante inicial es negativa, lo que indica que la partícula se está frenando. La celeridad alcanza un mínimo en el vértice de la parábola y a partir de ahí comienza a aumentar. En el punto de impacto la aceleración tangencial es positiva, lo que indica que la partícula se mueva cada vez más rápido.

En forma vectorial la aceleración tangencial es

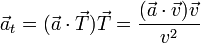
\vec{a}_t = (\vec{a}\cdot\vec{T})\vec{T}=\frac{(\vec{a}\cdot\vec{v})\vec{v}}{v^2}

que nos da

Instante inicial
\vec{a}_{t1}=-g\,\mathrm{sen}\,\alpha(\cos\alpha\vec{\imath}+\,\mathrm{sen}\,\alpha\vec{k})
Punto de máxima altura
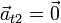
\vec{a}_{t2}=\vec{0}\,
Punto de impacto
\vec{a}_{t3}=g\,\mathrm{sen}\,\alpha(\cos\alpha\vec{\imath}-\,\mathrm{sen}\,\alpha\vec{k})

4.2 Aceleración normal

Una vez que tenemos la aceleración tangencial en cada uno de los tres puntos calculamos la aceleración normal restando

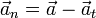
\vec{a}_n = \vec{a}-\vec{a}_t

Lo que nos da, en cada uno de los tres casos que estamos considerando

Instante inicial
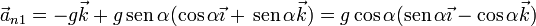
\vec{a}_{n1}=-g\vec{k}+g\,\mathrm{sen}\,\alpha(\cos\alpha\vec{\imath}+\,\mathrm{sen}\,\alpha\vec{k})=g\cos\alpha(\mathrm{sen}\,\alpha\vec{\imath}-\cos\alpha\vec{k})
Punto de máxima altura
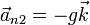
\vec{a}_{n2}=-g\vec{k}
Punto de impacto
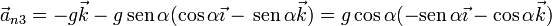
\vec{a}_{n3}=-g\vec{k}-g\,\mathrm{sen}\,\alpha(\cos\alpha\vec{\imath}-\,\mathrm{sen}\,\alpha\vec{k})=g\cos\alpha(-\mathrm{sen}\,\alpha\vec{\imath}-\cos\alpha\vec{k})

En módulo, estas tres aceleraciones normales valen

Instante inicial
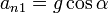
a_{n1}=g\cos\alpha\,
Punto de máxima altura
a_{n2}=g\,
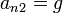
Punto de impacto
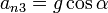
a_{n3}=g\cos\alpha\,

4.3 Vector normal

El vector unitario normal lo hallamos dividiendo la aceleración normal por su módulo

\vec{N}=\frac{\vec{a}

Obtenido de "http://tesla.us.es/wiki/index.php/Cinem%C3%A1tica_del_tiro_parab%C3%B3lico"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace