Cinemática de la partícula (G.I.T.I.)
De Laplace
(Diferencias entre revisiones)
(→Posición instantánea) |
(→Posición instantánea) |
||
| Línea 12: | Línea 12: | ||
<center><math>\vec{r}(t) = x(t)\vec{\imath}+y(t)\vec{\jmath}+z(t)\vec{k}</math></center> | <center><math>\vec{r}(t) = x(t)\vec{\imath}+y(t)\vec{\jmath}+z(t)\vec{k}</math></center> | ||
| - | Aquí <math>x(t)</math>, <math>y(t)</math> y <math>z(t)</math> son ciertas funciones continuas del tiempo | + | Aquí <math>x(t)</math>, <math>y(t)</math> y <math>z(t)</math> son ciertas funciones continuas del tiempo. |
==Velocidad y aceleración== | ==Velocidad y aceleración== | ||
Revisión de 10:09 28 may 2010
Contenido |
1 Introducción
1.1 Cinemática
1.2 Partícula
1.3 Sistema de referencia
2 Trayectoria y ley horaria
2.1 Posición instantánea
Cuando una partícula se mueve por el espacio en cada instante ocupará una posición, que irá cambiando de forma continua con el tiempo (ya que la partícula no puede dematerializarse o teleportarse a otra posición).
En principio podemos etiquetar cada posición por una letra A, B, C,... Sin embargo, es más práctico identificar cada posición por su vector de posición cuyas componentes cartesianas son las distancias a los planos coordenados
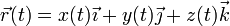
Aquí x(t), y(t) y z(t) son ciertas funciones continuas del tiempo.





