Transformación de energía potencial gravitatoria en calor
De Laplace
| Línea 24: | Línea 24: | ||
</math> | </math> | ||
</center> | </center> | ||
| - | donde <math>L_f</math> es | + | donde <math>L_f</math> es la entalpía de fusión del hielo a 1 atmósfera de presión. Entonces la fracción de masa derretida es |
<center> | <center> | ||
<math> | <math> | ||
| Línea 38: | Línea 38: | ||
</center> | </center> | ||
| - | [[Categoría:Problemas | + | [[Categoría:Problemas del primer principio de la termodinámica]] |
Revisión de 22:52 11 may 2010
Aquí tenemos una situación en que la energía mecánica se transforma en calor. Cuando el bloque está a una altura h sobre el suelo, tiene energía potencial gravitatoria. Al comenzar a caer esa energía potencial se va transformando en energía cinética. Y cuando choca con el suelo, una fracción λ de la energía cinética que tiene en el momento del impacto se transforma en calor absorbible por el hielo. Como éste esta a una temperatura de 0oC, este calor absorbido se invierte en derretir una parte de la masa de hielo.
Vamos a llamar h a la altura inicial del bloque de hielo, m a su masa y g a la aceleración de la gravedad. En el momento de impactar con el suelo su energía cinética es
Ec = mgh
Si se absorbe una fracción λ de esa energía en forma de calor tenemos
Q = λmgh
La masa de hielo que se funde es
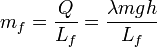
donde Lf es la entalpía de fusión del hielo a 1 atmósfera de presión. Entonces la fracción de masa derretida es
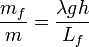
Utilizando los datos del problema (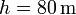 , λ = 0.02) y el valor
, λ = 0.02) y el valor 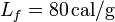 obtenemos
obtenemos