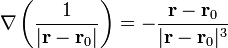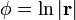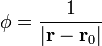Regla de la cadena para gradientes

De Laplace

(Diferencias entre revisiones)

última version al 19:15 13 abr 2010

Contenido

1 Enunciado
2 Solución

1 Enunciado

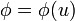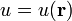Si $\phi = \phi(u)\,$ , con $u = u(\mathbf{r})$ , demuestre que

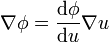
$\nabla \phi = \frac{\mathrm{d}\phi}{\mathrm{d}u} \nabla u$

Encuentre 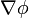$\nabla \phi$ si

$\phi=\ln|\mathbf{r}|\,$
$\phi =r^n\,$
$\phi=\frac{1}{|\mathbf{r} -\mathbf{r}_0|}$

2 Solución

2.1 Demostración

Para demostrar esto, recordamos que el gradiente se define como el único vector que, sea cual sea la dirección tomada, la derivada direccional puede calcularse como

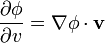
$\frac{\partial \phi}{\partial v} = \nabla\phi\cdot\mathbf{v}$

Por la definición de derivada direccional tenemos que

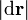$\frac{\partial \phi}{\partial v} = \frac{\mathrm{d}\phi}{|\mathrm{d}\mathbf{r}|}$

siendo $|\mathrm{d}\mathbf{r}|$ un desplazamiento infinitesimal en la dirección de 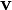$\mathbf{v}$ . Si en la expresión anterior multiplicamos y dividimos por $d u$ , el incremento en u cuando realizamos dicho desplazamiento, queda

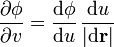
$\frac{\partial \phi}{\partial v} = \frac{\mathrm{d}\phi}{\mathrm{d}u}\,\frac{\mathrm{d}u}{|\mathrm{d}\mathbf{r}|}$

El primer factor es la derivada de 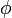$\phi\,$ respecto a $u$ , mientras que el segundo es la derivada direccional de $u$ en la dirección de 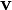$\mathbf{v}$ , por tanto

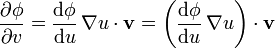
$\frac{\partial \phi}{\partial v} = \frac{\mathrm{d}\phi}{\mathrm{d}u}\,\nabla u\cdot\mathbf{v}= \left(\frac{\mathrm{d}\phi}{\mathrm{d}u}\,\nabla u\right)\cdot\mathbf{v}$

pero puesto que 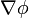$\nabla\phi$ es el único vector que al multiplicarlo por 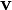$\mathbf{v}$ nos da la derivada direccional de 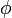$\phi\,$ se llega a la conclusión de que

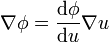
$\nabla\phi = \frac{\mathrm{d}\phi}{\mathrm{d}u}\nabla u$

2.2 Primer caso

Empleando este teorema es posible calcular multitud de gradientes. Así los correspondientes a los apartados 1 y 2 se pueden obtener a partir del de la función $u = r$ .

Para cualquier potencia de $r$ se tendrá

$\nabla(r^n)=\frac{\partial r^n}{\partial r}\nabla r=nr^{n-1}\nabla r$

por lo que el problema se reduce a calcular 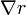$\nabla r$ . Si aplicamos la fórmula anterior a $r 2$ queda

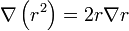
$\nabla\left(r^2\right)=2r\nabla r$

pero

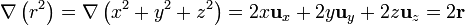
$\nabla\left(r^2\right)=\nabla\left(x^2+y^2+z^2\right)= 2x\mathbf{u}_{x}+2y\mathbf{u}_{y}+2z\mathbf{u}_{z}=2\mathbf{r}$

por lo que, igualando las dos expresiones,

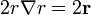
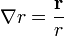
$2r\nabla r=2\mathbf{r}$ $\Rightarrow$ $\nabla r=\frac{\mathbf{r}}{r}$

y, para cualquier potencia de $r$

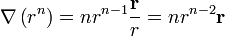
$\nabla\left(r^n\right)=nr^{n-1}\frac{\mathbf{r}}{r}=nr^{n-2}\mathbf{r}$

2.3 Segundo caso

Para el caso del logaritmo se tiene

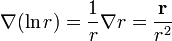
$\nabla(\ln r)=\frac{1}{r}\nabla r=\frac{\mathbf{r}}{r^2}$

Un método alternativo para estos dos casos es empleando coordenadas esféricas

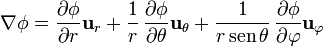
$\nabla\phi = \frac{\partial \phi}{\partial r}\mathbf{u}_{r}+\frac{1}{r}\,\frac{\partial \phi}{\partial \theta}\mathbf{u}_{\theta}+ \frac{1}{r\,\mathrm{sen}\,\theta}\,\frac{\partial \phi}{\partial \varphi}\mathbf{u}_{\varphi}$

Para el caso de una función que depende exclusivamente de la distancia al origen (un campo central), el gradiente se reduce a

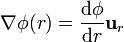
$\nabla\phi(r) = \frac{\mathrm{d}\phi}{\mathrm{d}r}\mathbf{u}_{r}$

que para 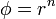$\phi=r^n\,$ da

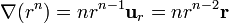
$\nabla(r^n)= n r^{n-1} \mathbf{u}_{r} = n r^{n-2}\mathbf{r}$

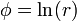
y para $\phi=\ln(r)\,$

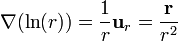
$\nabla(\ln(r)) = \frac{1}{r}\mathbf{u}_{r} = \frac{\mathbf{r}}{r^2}$

2.4 Tercer caso

Para la última función efectuamos un cálculo análogo, notando que

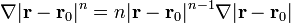
$\nabla |\mathbf{r}-\mathbf{r}_0|^n=n|\mathbf{r}-\mathbf{r}_0|^{n-1}\nabla|\mathbf{r}-\mathbf{r}_0|$

$\nabla|\mathbf{r}-\mathbf{r}_0|^2=\nabla\left(\left(\mathbf{r}-\mathbf{r}_0\right){\cdot}\left(\mathbf{r}-\mathbf{r}_0\right)\right) =\nabla\left(r^2-2\mathbf{r}{\cdot}\mathbf{r}_0+\mathbf{r}_0^2\right)$

El gradiente del primer término es conocido

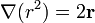
$\nabla(r^2) = 2\mathbf{r}$

El segundo, de acuerdo con lo que se demuestra en un problema de identidades vectoriales

$\nabla(2\mathbf{r}{\cdot}\mathbf{r}_0) = 2\mathbf{r}_0$

El tercer sumando se anula, por ser un vector constante

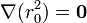
$\nabla(r_0^2) = \mathbf{0}$

Reuniendo los tres términos

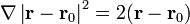
$\nabla\left|\mathbf{r}-\mathbf{r}_0\right|^2 = 2(\mathbf{r}-\mathbf{r}_0)$

y de aquí

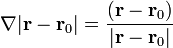
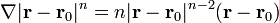
$\nabla|\mathbf{r}-\mathbf{r}_0| = \frac{(\mathbf{r}-\mathbf{r}_0)}{|\mathbf{r}-\mathbf{r}_0|}$ $\Rightarrow$ $\nabla |\mathbf{r}-\mathbf{r}_0|^n=n|\mathbf{r}-\mathbf{r}_0|^{n-2}(\mathbf{r}-\mathbf{r}_0)$

y, en particular

$\nabla\left(\frac{1}{|\mathbf{r}-\mathbf{r}_0|}\right)= -\frac{\mathbf{r}-\mathbf{r}_0}{|\mathbf{r}-\mathbf{r}_0|^3}$

@@ Línea 28: / Línea 28: @@
 <center><math>\frac{\partial \phi}{\partial v} = \frac{\mathrm{d}\phi}{\mathrm{d}u}\,\nabla u\cdot\mathbf{v}=  \left(\frac{\mathrm{d}\phi}{\mathrm{d}u}\,\nabla u\right)\cdot\mathbf{v} </math></center>
-pero puesto que <math>\nabla\phi</math> es el único vector que al multiplicarlo por <math>\mathbf{v}</math> nos da la derivada direccional de \phi\, se llega a la conclusión de que
+pero puesto que <math>\nabla\phi</math> es el único vector que al multiplicarlo por <math>\mathbf{v}</math> nos da la derivada direccional de <math>\phi\,</math> se llega a la conclusión de que
 <center><math>\nabla\phi = \frac{\mathrm{d}\phi}{\mathrm{d}u}\nabla u</math></center>

Regla de la cadena para gradientes

De Laplace

última version al 19:15 13 abr 2010

Contenido

1 Enunciado

2 Solución

2.1 Demostración

2.2 Primer caso

2.3 Segundo caso

2.4 Tercer caso

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES