Presión en el interior del océano
De Laplace
(→Corrección debida a la variación de la densidad) |
(→Corrección debida a la variación de la densidad) |
||
| Línea 27: | Línea 27: | ||
con | con | ||
| - | <center><math>\rho_0=1024\frac{\mathrm{kg}}{\mathrm{m}^3}</math>{{qquad}}{qquad}}<math>\rho_h=1028\frac{\mathrm{kg}}{\mathrm{m}^3}</math></center> | + | <center><math>\rho_0=1024\frac{\mathrm{kg}}{\mathrm{m}^3}</math>{{qquad}}{{qquad}}<math>\rho_h=1028\frac{\mathrm{kg}}{\mathrm{m}^3}</math></center> |
En este caso, la variación de la presión con la profundidad cumple | En este caso, la variación de la presión con la profundidad cumple | ||
última version al 10:34 12 abr 2010
Contenido |
1 Enunciado
Calcule la presión absoluta a 1000 m de profundidad en el océano. Considere que la densidad del agua es 1024 kg/m³ y que el aire que hay encima ejerce una presión de 101.3 kPa. A esta profundidad, ¿qué fuerza debe ejercer el armazón de la escotilla circular, de radio 30.0 cm, de un submarino para contrarrestar la fuerza del agua?
2 Presión a una cierta profundidad
Podemos admitir que la densidad del agua prácticamente no varía con la profundidad (aunque existe un ligero incremento debido al descenso de la temperatura y aumento de la salinidad). En este caso, considerando el peso de una columna vertical sobre un punto situado a una profundidad h tenemos
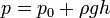
Sustituyendo
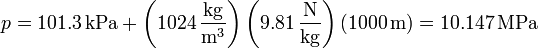
lo que equivale a unas 100 atmósferas.
3 Fuerza sobre una escotilla
La fuerza sobre una escotilla es debida a la diferencia de presiones entre sus dos caras. El interior del submarino se encuentra a una atmósfera, por lo que
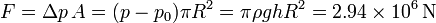
esto es, el equivalente a un peso de 289 toneladas situadas sobre la escotilla.
4 Corrección debida a la variación de la densidad
En los océanos, la densidad aumenta con la profundidad debido a la disminución de la temperatura y al aumento de la salinidad. Esta variación, conocida como picnoclina, está determinada experimentalmente de forma que en la superficie la densidad vale 1024 kg/m³ y a 1000 m vale 1028 kg/m³, siendo la variación aproximadamente lineal. Podemos entonces escribir la densidad como
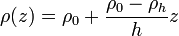
con
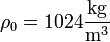
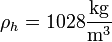
En este caso, la variación de la presión con la profundidad cumple
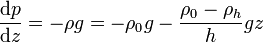
Integrando aquí
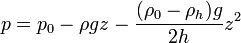
que en z = − h nos da
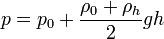
es decir, equivale a que consideremos una densidad uniforme de 1026 kg/m³ (la media entre los extremos). Esto da una presión
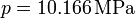
Vemos que la diferencia entre este resultado y el obtenido en el primer apartado es muy pequeña.





