Presión en el interior del océano
De Laplace
(Nueva página: ==Enunciado== Calcule la presión absoluta a 1000 m de profundidad en el océano. Considere que la densidad del agua es 1024 kg/m³ y que el aire que hay encima ejer...) |
(→Presión a una cierta profundidad) |
||
| Línea 9: | Línea 9: | ||
Sustituyendo | Sustituyendo | ||
| - | <center><math>p = 101.3\,\mathrm{kPa} + \left(1024\,\frac{\mathrm{kg}{m^3}\right)\left(9.81\,\frac{\mathrm{N}}{\mathrm{kg}}\right)(1000\,\mathrm{m}) = 10146.7\,\mathrm{kPa}</math></center> | + | <center><math>p = 101.3\,\mathrm{kPa} + \left(1024\,\frac{\mathrm{kg}}{\mathrm{m}^3}\right)\left(9.81\,\frac{\mathrm{N}}{\mathrm{kg}}\right)(1000\,\mathrm{m}) = 10146.7\,\mathrm{kPa}</math></center> |
==Fuerza sobre una escotilla== | ==Fuerza sobre una escotilla== | ||
Revisión de 11:21 12 abr 2010
Contenido |
1 Enunciado
Calcule la presión absoluta a 1000 m de profundidad en el océano. Considere que la densidad del agua es 1024 kg/m³ y que el aire que hay encima ejerce una presión de 101.3 kPa. A esta profundidad, ¿qué fuerza debe ejercer el armazón de la escotilla circular, de radio 30.0 cm, de un submarino para contrarrestar la fuerza del agua?
2 Presión a una cierta profundidad
Podemos admitir que la densidad del agua prácticamente no varía con la profundidad (aunque existe un ligero incremento debido al descenso de la temperatura y aumento de la salinidad). En este caso, considerando el peso de una columna vertical sobre un punto situado a una profundidad h tenemos
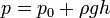
Sustituyendo
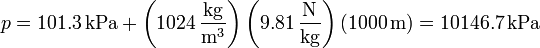
3 Fuerza sobre una escotilla
La fuerza sobre una escotilla es debida a la diferencia de presiones entre sus dos caras. El interior del submarino se encuentra a una atmósfera, por lo que
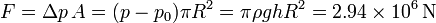
esto es, el equivalente a un peso de 289 toneladas situadas sobre la escotilla.
4 Corrección debida a la variación de la densidad
En los océanos, la densidad aumenta con la profundidad debido a la disminución de la temperatura y al aumento de la salinidad. Esta variación, conocida como picnoclina, está determinada experimentalmente de forma que en la superficie la densidad vale 1024 kg/m³





