Tubo de Venturi
De Laplace
(Nueva página: ==Enunciado== El ''tubo de Venturi'' se utiliza para medir la velocidad de un fluido incompresible. Consiste en un tubo con un estrechamiento, de modo que las secciones antes y despu...) |
|||
| Línea 3: | Línea 3: | ||
==Solución== | ==Solución== | ||
| + | La ley de conservación de la masa establece que en un flujo estacionario toda la masa que entra por un lado de un recinto debe salir por otro, lo que implica que la velocidad debe ser mayor en la parte más estrecha del tubo | ||
| + | |||
| + | <center><math>v_1A_1 = v_2A_2\,</math></center> | ||
| + | |||
| + | Por otro lado, la ley de Bernouilli establece que para dos puntos situados en la misma línea de corriente se cumple | ||
| + | |||
| + | <center><math>p_1 + \rho g y_1 + \frac{1}{2}\rho v_1^2 = p_2 + \rho g y_2 + \frac{1}{2}\rho v_2^2</math></center> | ||
| + | |||
| + | Si los dos puntos se encuentran a la misma altura la presión hidrostática es la misma para ambos, por lo que | ||
| + | |||
| + | <center><math>p_1 + \frac{1}{2}\rho v_1^2 = p_2 + \frac{1}{2}\rho v_2^2</math></center> | ||
| + | |||
| + | Reordenando términos | ||
| + | |||
| + | <center><math>v_1^2 - v_2^2 = \frac{2(p_2-p_1)}{\rho}</math></center> | ||
| + | |||
| + | Sustituimos la ecuación de conservación de la masa | ||
| + | |||
| + | <center><math>v_1^2\left(1-\frac{A_1^2}{A_2^2}\right)=\frac{2(p_2-p_1)}{\rho}</math>{{tose}} <math>v_1 = A_2\sqr{\frac{2(p_2-p_1)}{\rho(A_1^2-A_2^2)}}</math></center> | ||
| + | |||
| + | Análogamente | ||
| + | |||
| + | <center><math>v_2 = A_1\sqr{\frac{2(p_2-p_1)}{\rho(A_1^2-A_2^2)}}</math></center> | ||
| + | |||
| + | y el flujo volumétrico es | ||
| + | |||
| + | <center><math>Q=A_1v_1 = A_2v_2 = A_1A_2\sqr{\frac{2(p_2-p_1)}{\rho(A_1^2-A_2^2)}}</math></center> | ||
| + | |||
| + | |||
| + | |||
| + | |||
[[Categoría:Problemas de introducción a la mecánica de fluidos]] | [[Categoría:Problemas de introducción a la mecánica de fluidos]] | ||
Revisión de 11:46 10 abr 2010
1 Enunciado
El tubo de Venturi se utiliza para medir la velocidad de un fluido incompresible. Consiste en un tubo con un estrechamiento, de modo que las secciones antes y después del estrechamiento son A1 y A2, con A1 > A2. En cada parte del tubo hay un manómetro, de modo que se pueden medir las presiones respectivas p1 y p2. Encuentra una expresión para la velocidad del fluido en cada parte del tubo en función del área de las secciones, las presiones y su densidad.
2 Solución
La ley de conservación de la masa establece que en un flujo estacionario toda la masa que entra por un lado de un recinto debe salir por otro, lo que implica que la velocidad debe ser mayor en la parte más estrecha del tubo
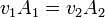
Por otro lado, la ley de Bernouilli establece que para dos puntos situados en la misma línea de corriente se cumple
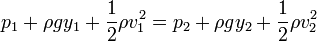
Si los dos puntos se encuentran a la misma altura la presión hidrostática es la misma para ambos, por lo que
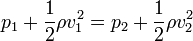
Reordenando términos
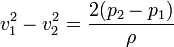
Sustituimos la ecuación de conservación de la masa
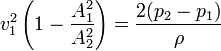
No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): v_1 = A_2\sqr{\frac{2(p_2-p_1)}{\rho(A_1^2-A_2^2)}}
Análogamente
y el flujo volumétrico es
