Generador
De Laplace
(→En circuito abierto) |
(→En circuito cerrado) |
||
| Línea 81: | Línea 81: | ||
===En circuito cerrado=== | ===En circuito cerrado=== | ||
| - | Cuando se | + | Cuando se cierra el circuito, parte de la carga del polo positivo fluye hacia el negativo (y viceversa) a través de la conexión 8que, puede ser una resistencia, un motor, o cualquier otro elemento o elementos). |
| - | + | ||
| + | Al haber una cierta recombinación de carga, el campo electrostático se ve reducido y ya no llega a compensar exactamente a la fuerza no electrostática, de forma que ahora se tiene, dentro del generador | ||
| + | |||
| + | <center><math>\mathbf{E}+\mathbf{E}'\neq\mathbf{0}\,</math></center> | ||
| + | |||
| + | En primera aproximación, podemos admitir que esta suma será una cantidad proporcional a la corriente que pasa por el generador. Si no hay corriente (circuito abierto), es nula, y si sí la hay, cuanta más corriente, más recombinación de carga y menor campo eléctrico. | ||
| + | |||
| + | <center><math>\mathbf{E}+\mathbf{E}'\propto I\,</math></center> | ||
| + | |||
| + | Esta relación de proporcionalidad deja de ser cierta cuando la corriente que pasa por el generador es muy intensa (lo que ocurre en cortocircuito). | ||
| + | |||
| + | Si colocamos de nuevo un voltímetro (sin desconectar el generador del circuito al que está alimentando, y volvemos a calcular la f.e.m. a lo largo de una curva que pasa por la fuente y el voltímetro obtenemos | ||
<center><math>V_P-V_N = \mathcal{E} - I r\,</math></center> | <center><math>V_P-V_N = \mathcal{E} - I r\,</math></center> | ||
Revisión de 16:36 28 mar 2010
Contenido |
1 Introducción
Consideremos un circuito cerrado, por el cual fluye una corriente estacionaria. La potencia desarrollada por unidad de volumen por un campo eléctrico es de la forma  , siendo el balance neto
, siendo el balance neto
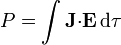
En el estado estacionario, la energía es una constante y esta integral debe ser nula. En las regiones donde hay corrientes óhmicas, esta potencia es siempre positiva, por lo que el sistema pierde energía (como sabemos, en forma de calor). Descomponiendo la integral en las regiones óhmicas y en el resto tendremos que
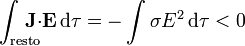
Este balance implica que debe haber algún punto a lo largo del circuito en el que la densidad de corriente vaya en la dirección opuesta al campo eléctrico. Es estos puntos, el movimiento de las cargas no será producido por el propio campo electrostático, sino por algún otro agente de origen no eléctrico o, si es eléctrico, no irrotacional, que mueva las cargas y aporte la energía perdida. Un campo eléctrico irrotacional es conservativo y no puede dar cuenta de estas pérdidas.
Otra forma de llegar a la misma conclusión es notar que, en una situación estacionaria, el campo eléctrico es irrotacional y, por tanto, sus líneas de campo son abiertas. La densidad de corriente, en cambio, es solenoidal y (para un circuito cerrado) posee líneas de campo cerradas. Se deduce que en algún punto a lo largo del circuito, deben tener orientaciones contrarias.
2 Definición de generador
Un generador es entonces un dispositivo que puede producir una corriente eléctrica ejerciendo una fuerza no electrostática sobre las cargas eléctricas. Debe ser no electrostática pues un campo electrostático no puede producir trabajo neto sobre una curva cerrada y por tanto no puede mantener una corriente en un circuito cerrado. Como ejemplos de estas fuerzas tenemos fuerzas magnéticas, químicas o mecánicas, e incluso eléctricas (no estáticas).
Esta fuerza mueve a las cargas situadas en el interior del generador, separándolas y creando la aparición de un polo positivo (o ánodo) y uno negativo (o cátodo).
La naturaleza de las fuerzas no eléctricas sobre las cargas eléctricas dentro de los generadores puede ser muy diversa. Aquí es suficiente para nuestro propósito explicar cualitativamente los tres tipos más comunes de estas fuerzas.
- Fuerzas mecánicas
- El ejemplo más sencillo es el constituido por las fuerzas mecánicas, en las que se basa el llamado generador de Van de Graaf. Éste consiste en una banda de goma aislante que se carga por fricción o por precipitación de cargas. La banda transporta la carga fijada a su superficie hasta una cúpula metálica conductora. De esta forma se produce una separación de la carga. Si esta cúpula se uniera por algún conductor a tierra, se produciría una corriente óhmica en sentido contrario al arrastre por la banda de goma. Este mismo principio explica la electrización de los jugadores de baloncesto en un día seco.
- Pilas químicas
- Históricamente, el primer conjunto de fuentes de fuerzas electromotrices, capaces de producir corrientes de suficiente intensidad, y por un período significativo de tiempo, fueron las células químicas. Básicamente consisten en lo siguiente: consideremos un cuerpo metálico inmerso en una solución conductora del mismo componente químico. El cuerpo metálico se denomina electrodo y la solución electrolito. En una delgada capa de contacto entre electrodo y electrolito, actúan sobre las cargas eléctricas ciertas fuerzas. Estas fuerzas tienen diferente magnitud e incluso diferentes direcciones para distintos pares de electrodos y electrolitos. Por tanto, si dos electrodos de diferente material se sumergen en el mismo electrolito, estas fuerzas actuarán desde un electrodo hacia el electrolito, y desde el electrolito hacia el otro electrodo. Si los electrodos están conectados por conductores metálicos, actuarán como una bomba hidráulica que empuja las cargas eléctricas en la misma dirección.
- Fuerzas magnéticas
- Una carga en movimiento en el seno de un campo magnético experimenta una fuerza magnética dada por la ley de Lorentz. Un ejemplo de aplicación de fuerzas magnéticas para producir corrientes continuas lo constituye el geenrador homopolar o disco de Faraday.
- Inducción
- Un campo magnético variable en el tiempo, de acuerdo con la ley de Faraday produce un campo eléctrico no irrotacional, capaz de mantener cargas en movimiento a lo largo de un circuito. En este principio se basan la mayoría de los generadores industriales, como alternadores y dinamos.
En conclusión, sobre las cargas eléctricas libres actúan, en cualquier punto, simultáneamente fuerzas eléctricas y fuerzas no eléctricas. Las primeras son debidas al campo eléctrico originado por la distribución de cargas, pero las últimas no son producidas por dichas cargas.
Las fuerzas no eléctricas son llamadas usualmente fuerzas externas, de forma que se verifica, para cada una de las cargas,
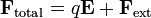
Ahora bien, 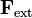 puede representarse como el producto de q por un cierto campo efectivo
puede representarse como el producto de q por un cierto campo efectivo  . Hay que hacer hincapié en que
. Hay que hacer hincapié en que 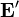 no define ningún campo electrostático, puesto que no es debido a cargas eléctricas estacionarias. De ahí,
no define ningún campo electrostático, puesto que no es debido a cargas eléctricas estacionarias. De ahí,

Igualmente se tendrá, para la densidad de corriente, si es aplicable la ley de Ohm,
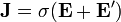
El campo eléctrico 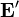 existe únicamente en el interior de las fuentes o generadores, mientras que el campo electrostático real
existe únicamente en el interior de las fuentes o generadores, mientras que el campo electrostático real  , debido a la distribución de cargas, existe dentro de las fuentes y fuera de ellas. Donde existe, el campo efectivo
, debido a la distribución de cargas, existe dentro de las fuentes y fuera de ellas. Donde existe, el campo efectivo 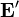 debe ir en dirección opuesta a
debe ir en dirección opuesta a  .
.
3 Definición de fuerza electromotriz
La acción neta de las fuerzas no electrostáticas que actúan en los generadores se mide con la fuerza electromotriz, cuya unidad es el voltio y definida como
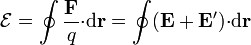
esto es, la integral a lo largo de una curva cerrada de la fuerza total por unidad de carga. En términos físicos, representa el trabajo por unidad de carga para hacer que una carga de prueba diera una vuelta completa al circuito.
Esta fuerza total incluye al campo electrostático  como al campo efectivo
como al campo efectivo 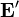 . Sin embargo, dado que el campo electrostático es conservativo, se cumple
. Sin embargo, dado que el campo electrostático es conservativo, se cumple
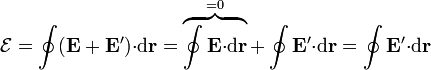
es decir, el valor neto de la fuerza electromotriz depende solo de la fuerza externa no electrostática que actúa sobre las cargas.
4 Relación con el voltaje
Dado que la fuerza electromotriz es un voltaje, nos preguntamos popr su relación con la diferencia de potencial entre los polos del generador
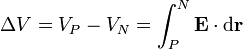
que es la cantidad que se mide desde el exterior con un voltímetro.
4.1 En circuito abierto
Supongamos un generador en circuito abierto, esto es, no hay nada conectado a sus polos, y no hay corriente pasando por su interior.
En este caso la fuerza externa separa a las cargas, apareciendo una densidad de carga positiva en el ánodo y negativa en el cátodo. El proceso de acumulación se detiene cuando la fuerza electrostática debido a esta densidad de carga anula completamente la acción de la fuerza externa, de manera que dentro del generador


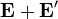
Fuera del generador hay campo electrostático (que se extiende a todo el espacio, no solo al interior del generador, pero la fuerza no electrostática es nula.
En este caso podemos calcular la fuerza electromotriz a lo largo de una curva cerrada Γ que pasa por el interior entrando por el polo negativo y saliendo por el positivo, y por el exterior sigue un camino arbitrario de P a N. En particular, si tenemos un voltímetro conectado a los bornes, con el polo positivo del voltímetro conectado al polo positivo del generador, tomamos el camino que pasa por el interior del voltímetro. Resulta

esto es, la fuerza electromotriz coincide con la diferencia de potencial entre los polos en circuito abierto. Esto proporciona un procedimiento de medida de la f.e.m. Basta con emplear un voltímetro conectándolo a los polos del generador, sin que haya corriente circulando por el generador.
4.2 En circuito cerrado
Cuando se cierra el circuito, parte de la carga del polo positivo fluye hacia el negativo (y viceversa) a través de la conexión 8que, puede ser una resistencia, un motor, o cualquier otro elemento o elementos).
Al haber una cierta recombinación de carga, el campo electrostático se ve reducido y ya no llega a compensar exactamente a la fuerza no electrostática, de forma que ahora se tiene, dentro del generador
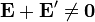
En primera aproximación, podemos admitir que esta suma será una cantidad proporcional a la corriente que pasa por el generador. Si no hay corriente (circuito abierto), es nula, y si sí la hay, cuanta más corriente, más recombinación de carga y menor campo eléctrico.

Esta relación de proporcionalidad deja de ser cierta cuando la corriente que pasa por el generador es muy intensa (lo que ocurre en cortocircuito).
Si colocamos de nuevo un voltímetro (sin desconectar el generador del circuito al que está alimentando, y volvemos a calcular la f.e.m. a lo largo de una curva que pasa por la fuente y el voltímetro obtenemos
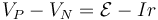
donde VP − VN es la diferencia de potencial entre bornes, I la corriente que atraviesa el generador y r la resistencia interna de éste.
Hay que remarcar que en el interior de un generador no se verifica la ley de Ohm, ya que la corriente o bien es nula o bien va en
sentido opuesto al campo eléctrico. En todo caso, se verifica 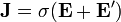 cuando el agente externo actúa en un medio óhmico.
cuando el agente externo actúa en un medio óhmico.
Modelando un generador real en un circuito equivalente, lo podemos considerar como compuesto de un generador ideal (sin resistencia interna) asociado en serie con una resistencia r.
Cuando se describe una curva cerrada en un sistema en estado estacionario, atravesando uno o varios generadores, la definición de fuerza electromotriz, trasladada al circuito equivalente, conduce a la ley de Kirchhoff para las mallas
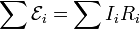
donde las Ii son las corrientes que circulan por las distintas ramas que recorremos, y las Ri incluyen también las resistencias internas de las fuentes.
5 Potencia de un generador
6 Modelo circuital de generador
6.1 Fuente de tensión
6.2 Fuente de intensidad
7 Ejemplos
7.1 Generador de Van de Graaf








