Rectas de regresión. Introducción

De Laplace

Revisión de 10:48 24 mar 2010

Introducción

En numerosas ocasiones no debemos determinar cuánto vale una cantidad directa o indirectamente, sino cómo depende una variable de otra.

A la hora de establecer una dependencia vamos variando una cierta magnitud x (a la que denominaremos entrada}) en una serie de valores x_i. Para cada uno de estos valores medimos un valor y_i de una magnitud y (la respuesta o salida). El resultado puede tabularse en una tabla de dos columnas, y representarse gráficamente.

Ejemplo

Supongamos que fijamos la tensión en los extremos de un cable y medimos la corriente que circula por él, obteniendo el siguiente resultado

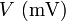
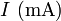
3.25	1.40
3.50	2.93
3.75	3.28
4.00	4.30
4.25	11.92
4.50	6.65
4.75	8.57
5.00	9.56
5.25	11.58
5.50	13.61
5.75	15.64

Es evidente, de este comportamiento, que existe una relación funcional entre x e y (I y V en este caso). Ahora bien, ¿qué función representa correctamente esta conducta, una recta, una parábola, una exponencial? Y, si se trata de una parábola, ¿cuáles son los coeficientes a, b, c de la función y = ax² + bx + c?

Además, sospechamos que el punto que se aparta mucho del resto es un error experimental y no debe ser tenido en cuenta. Sin embargo, ¿cómo podemos estar seguros de ello? Quizás la dependencia entre x e y sea muy compleja y el punto separado sea correcto.

Este tipo de problema se denomina ajuste de una función y como vemos puede ser extremadamente complicado, dependiendo del tipo de función y del número de datos y parámetros empleados para describirla.

Aquí nos limitaremos al caso más simple: el ajuste de una recta por el método de mínimos cuadrados. Partimos de una serie de datos más o menos alineados y trataremos de buscar la recta que pasa más cerca de ellos.

Este tipo de ajuste es de interés en varias situaciones diferentes

1. Cuando tenemos una serie de entradas y salidas, para las cuales no sabemos si existe una relación funcional, pero lo sospechamos, como en la figura anterior. En este caso, la bondad de la recta de regresión (esto es, cuánto se aproxima a los datos) nos informa de si esta relación existe o no.
2. Cuando tenemos un conjunto de datos, de los cuales sabemos con seguridad que deberían estar alineados y queremos emplear la recta de mejor ajuste para determinar alguna cantidad indirecta. Por ejemplo, supongamos que conocemos una serie de pares de valores de tensión V frente a intensidad de corriente I para un cable y queremos determinar la resistencia de acuerdo con la ley de Ohm, V = IR. En lugar de determinar una resistencia para cada dato, buscaremos la recta de mejor ajuste, cuya pendiente será la resistencia buscada.
3. Las rectas de mejor ajuste también pueden usarse para hallar el valor de la salida para entradas que no hayamos medido experimentalmente. Esto es lo que se conoce como interpolación si x se encuentra en el mismo intervalo que los datos experimentales y extrapolación si está fuera de éste.
4. Cuando tenemos un conjunto de datos para los cuales existe una relación funcional complicada, como la ilustrada en la figura, pero para la cual sabemos que en determinadas regiones, más o menos grandes, la conducta es aproximadamente lineal. En este caso, si nos restringimos a una de estas regiones, podemos aproximar la función por la recta de mejor ajuste, lo que simplifica los cálculos. Por supuesto, en este caso la recta de mejor ajuste dependerá de la región en que nos encontremos, por lo que deberemos ser conscientes en todo momento de los límites de validez de la aproximación que empleemos. En estas aproximaciones también podemos emplear la recta de mejor ajuste para interpolar. Sin embargo, las extrapolaciones son mucho más arriesgadas, ya que podemos salirnos de los límites de validez.