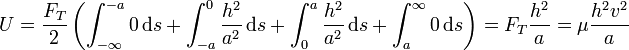Potencia y energía en una onda
De Laplace
(→Onda triangular) |
(→Onda triangular) |
||
| Línea 163: | Línea 163: | ||
<center><math> | <center><math> | ||
| - | U = \frac{F_T}{2}\left(\int_{-\infty}^{-a}0\,\mathrm{d}s+\int_{-a}^{0}\frac{h^2}{a^2}\,\mathrm{d}s+\int_{0}^{a}\frac{h^2}{a^2}\,\mathrm{d}s+\int_{a}^{\infty}0\,\mathrm{d}s\right) = F_T \frac{h^2}{a}=\mu\frac{ | + | U = \frac{F_T}{2}\left(\int_{-\infty}^{-a}0\,\mathrm{d}s+\int_{-a}^{0}\frac{h^2}{a^2}\,\mathrm{d}s+\int_{0}^{a}\frac{h^2}{a^2}\,\mathrm{d}s+\int_{a}^{\infty}0\,\mathrm{d}s\right) = F_T \frac{h^2}{a}=\mu\frac{h^2v^2}{a}</math></center> |
===Energía total=== | ===Energía total=== | ||
Revisión de 12:40 23 mar 2010
Contenido |
1 Introducción
Una onda suele definirse en términos como una “transmisión de energía sin transmisión de materia”. Esta definición, aunque un tanto imprecisa y no lo bastante general (ya que no incluye, por ejemplo, a las ondas estacionarias), sí expresa un hecho cierto: una onda viajera transmite energía desde el punto en que se origina hasta el punto al que llega, actuando como mecanismo para la “acción a distancia”.
Un cierto agente desarrolla una potencia al emitir una onda (sea ésta en una cuerda, de sonido, electromagnética o de otro tipo), esta potencia se manifiesta en una cierta densidad de energía que se propaga a lo largo de la onda y es entregada en el punto de destino a través de la potencia desarrollada por el propio medio de propagación (por ejemplo, la fuerza que ejerce una cuerda sobre un sistema situado en su extremo final.
Esta propagación es simultánea al almacenamiento de energía. La energía se propaga gracias a que en todo momento hay una cierta energía almacenada a lo largo del medio. En particular, en las ondas estacionarias tenemos almacenamiento de energía sin propagación.
A continuación nos centraremos en el caso particular de la cuerda tensa, con especial atención a las ondas sinusoidales, aunque muchos de los resultados son generalizables a otros tipos de ondas.
2 Energía almacenada
2.1 Energía cinética
La energía cinética almacenada en un instante dado en una longitud dada de la cuerda es la suma de las energías cinéticas de cada una de las partículas que la forman.
Si dividimos la cuerda en porciones de longitud dx, la masa de cada porción es
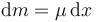
con μ la densidad lineal de masa. La energía cinética de esta pedazo será
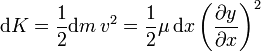
Integrando obtenemos la energía cinética almacenada en una porción de cuerda
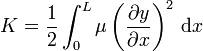
2.1.1 Onda viajera sinusoidal
Aplicando la ecuación anterior a una longitud de onda de una onda viajera
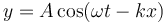
obtenemos la energía cinética de una porción de cuerda
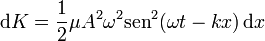
y la integral sobre una longitud de onda
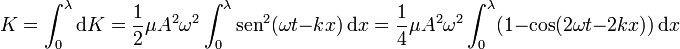
donde hemos usado la fórmula del ángulo doble
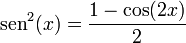
Resultan dos integrales, la primera de las cuales vale simplemente λ, mientras que la segunda es una integral de cos(s) sobre dos periodos, por lo que se anula. Por tanto
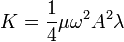
Lo más importante de este resultado es que resulta una función cuadrática en la amplitud, esto es, a doble amplitud corresponde cuádruple energía.
Una cantidad derivada de esta es la densidad de energía cinética, obtenida suponiendo que la energía cinética se reparte uniformemente sobre la longitud de onda (lo cual es cierto solo en promedio).
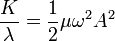
Esta densidad de energía no solo es cuadrática en en la amplitud, sino también la frecuencia.
2.1.2 Onda estacionaria sinusoidal
De forma análoga se calcula la energía cinética de la onda estacionaria
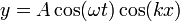
y resulta
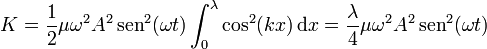
A diferencia del caso de la onda viajera, para el cual la energía cinética permanece constante en el tiempo, en la onda estacionaria resulta una cantidad oscilante. La razón es que para una onda viajera en una longitud de onda hay en todo momento puntos con velocidad máxima y puntos en reposo, y todas las posibilidades intermedias. En una onda estacionaria todos los puntos oscilan al unísono de forma que en un instante todos tienen la velocidad máxima (y la energía cinética es máxima), y en otro están todos en reposo (y la energía cinética es nula).
2.1.3 Onda triangular
Consideremos ahora el caso de un pulso triangular
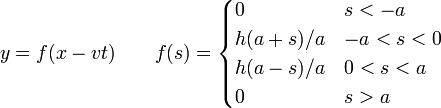
y vamos a calcular la energía almacenada en toda la longitud de la onda (desde  hasta
hasta  )
)
La velocidad de cada punto es
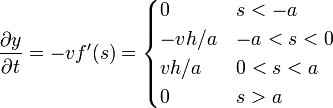
y la energía cinética
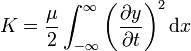
haciendo el cambio de variable s = x − vt y separando la integral en cuatro tramos queda
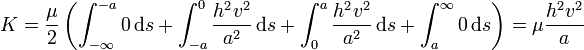
2.2 Energía potencial
Una onda también almacena energía potencial ya que al deformarse se estira, almacenando energía elástica.
La energía potencial almacenada entre los puntos x y x + dx es el trabajo realizado al aumentar la longitud de un trozo de dx a ds
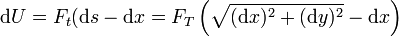
donde hemos aplicado el teorema de Pitágoras para expresar ds.
Si la deformación es pequeña, ds y dx son cantidades muy próximas, por lo que la expresión de arriba tiende a cero. Para evitar quedarnos sin nada, multiplicamos arriba y abajo por ds + dx y nos queda
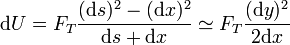
La variación de y la da la derivada
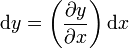
lo que nos da el diferencial de energía potencial
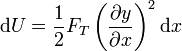
y la energía potencial contenida en una una cierta longitud de cuerda
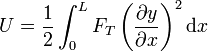
2.2.1 Onda viajera sinusoidal
La energía potencial almacenada en una longitud de onda de la onda viajera
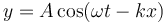
es
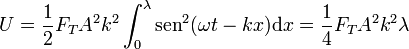
y densidad de energía potencial por unidad de longitud
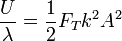
Aplicando que
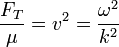
esta densidad de energía se transforma en
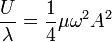
esto es, es idéntica a la densidad de energía cinética.
2.2.2 Onda estacionaria sinusoidal
De la misma manera podemos calcular la energía potencial de una onda estacionaria
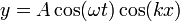
y resulta
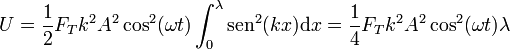
Aplicando de nuevo la relación entre la tensión y la velocidad de la onda
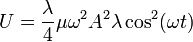
Como con la energía cinética, la energía potencial de una onda estacionaria es una constante. Es la suma de las dos, la energía mec´ánica, la que permanece constante.
2.2.3 Onda triangular
Para el pulso triangular
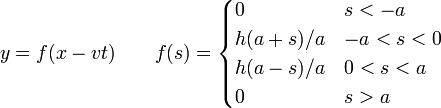
la energía potenical almacenada en toda la longitud de la onda (desde  hasta
hasta 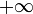 ) es
) es
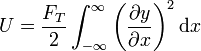
La derivada que aparece en el integrando es igual a
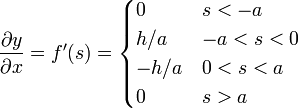
haciendo el cambio de variable s = x − vt y separando la integral en cuatro tramos queda