Ondas estacionarias
De Laplace
(→En un extremo fijo) |
(→En un extremo fijo) |
||
| Línea 47: | Línea 47: | ||
<center><math>0 = y(x=0) = f(t)+g(t)\,</math>{{tose}} <math>g(t) = -f(t)\,</math></center> | <center><math>0 = y(x=0) = f(t)+g(t)\,</math>{{tose}} <math>g(t) = -f(t)\,</math></center> | ||
| - | [[Imagen:Reflexionpulso.gif| | + | [[Imagen:Reflexionpulso.gif|450px|right]] |
y la solución para el resto de los puntos es | y la solución para el resto de los puntos es | ||
Revisión de 13:15 14 mar 2010
Contenido |
1 Superposición de ondas
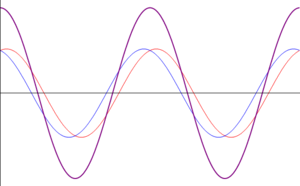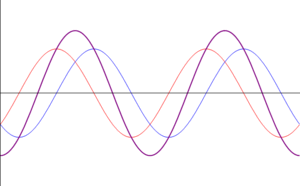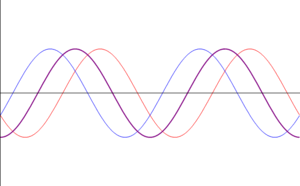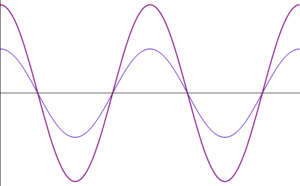
Vamos a examinar ahora el caso de que tengamos dos ondas viajeras de la misma frecuencia y amplitud y propagándose en sentidos opuestos:
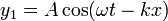
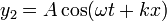
En este caso no es necesario introducir la constante 
porque, para ondas que van en sentidos opuestos el concepto de desfase no tiene mucho sentido. Se puede incluir esta constante, pero los resultados no se diferencian en lo esencial de lo que se obtiene sin ella.
La superposición de estas dos señales se puede transformar aplicando relaciones trigonométricas
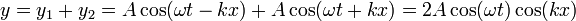
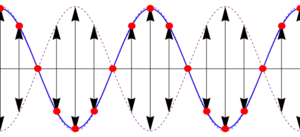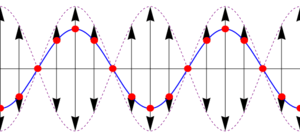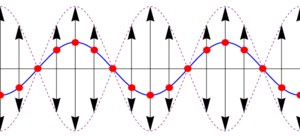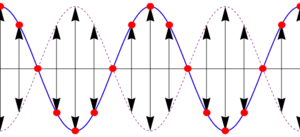
Esta es la ecuación de una onda estacionaria, que se puede escribir en la forma
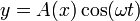
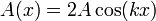
Lo que nos dice esta ecuación es que aunque tenemos la superposición de dos ondas viajeras, la suma es una onda en que todos los puntos oscilan en fase, con una amplitud dependiente de su posición. En los puntos en que resulta una amplitud A(x) negativa, debe entenderse que la amplitud es el valor absoluto de esta cantidad y que los puntos correspondientes están en oposición de fase (esto es, tienen una constante de fase igual a π).
- Nodos
- La amplitud varía como un coseno, lo cual implica que existen puntos para los cuales la amplitud de oscilación es nula. Estos puntos se denominan nodos. La posición de estos nodos la da la condición
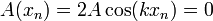
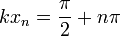
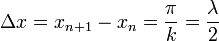
- La distancia entre nodos consecutivos es media longitud de onda
- Vientres
- Los puntos en que la amplitud de oscilación es máxima se denominan vientres. Los vientres se encuentran en los puntos medios entre nodos, y por tanto la distancia entre vientres consecutivos es también media longitud de onda, y la distancia de un vientre al nodo más próximo es λ / 4.
2 Reflexión de ondas
2.1 En un extremo fijo
Supongamos una cuerda tensa sujeta por un extremo a un punto fijo, como un clavo en una pared. Esto hace que la elongación de dicho punto sea nula en todo instante
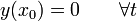
esto es, el punto x = x0 es un nodo de la onda.
Por ello, no es posible que la solución de la ecuación de ondas en este sistema sea simplemente una onda viajera y = f(x − vt), ya que esta solución se hará diferente de cero en x0 en algún momento.
Para poder imponer que la elongación sea nula debemos considerar la superposición de dos ondas, una viajando hacia la derecha y otra hacia la izquierda
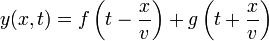
Por simplicidad, supongamos que x0 = 0. Puesto que en este punto y = 0 en todo instante, debe cumplirse
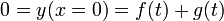
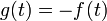
y la solución para el resto de los puntos es
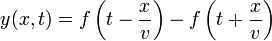
esto es, la señal completa es la superposición de una onda viajera hacia la derecha, más una onda viajera, igual y de signo opuesto, viajando en sentido contrario
