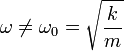Oscilaciones forzadas
De Laplace
(Diferencias entre revisiones)
(→Introducción) |
(→Solución) |
||
| Línea 20: | Línea 20: | ||
<center><math>\omega\neq \omega_0=\sqrt{\frac{k}{m}}</math></center> | <center><math>\omega\neq \omega_0=\sqrt{\frac{k}{m}}</math></center> | ||
| - | ==Solución== | + | ==Solución estacionaria== |
===Posición=== | ===Posición=== | ||
===Velocidad=== | ===Velocidad=== | ||
| + | |||
==Dependencia con la frecuencia== | ==Dependencia con la frecuencia== | ||
===Amplitud=== | ===Amplitud=== | ||
Revisión de 12:23 10 mar 2010
Contenido |
1 Introducción
Un oscilador armónico amortiguado es aquel que, en adición a la fuerza recuperadora dada por la ley de Hooke, experimenta una fuerza de rozamiento viscoso proporcional a la velocidad.
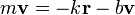
Si este oscilador se mueve a lo largo de una recta, la segunda ley de Newton se reduce a

Si este oscilador amortiguado se encuentra sometido a una fuerza externa adicional, en general dependiente del tiempo, se dice que el oscilador está forzado, siendo su ecuación de movimiento
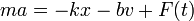
De entre los posibles tipos de fuerza que se pueden aplicar, la más importante desde el punto de vista físico, es aquella que en sí misma es oscilante, esto es

donde la frecuencia de oscilación de la fuerza no tiene por qué coincidir con la frecuencia propia del oscilador armónico