Momento cinético de una barra
De Laplace
(Diferencias entre revisiones)
(→Enunciado) |
(→Rotación en torno al centro) |
||
| Línea 10: | Línea 10: | ||
Tomamos un sistema de ejes fijos en el cual el origen de coordenadas es el centro de la barra, el eje Z es el eje instantáneo de rotación y X es el eje a lo largo de la barra. | Tomamos un sistema de ejes fijos en el cual el origen de coordenadas es el centro de la barra, el eje Z es el eje instantáneo de rotación y X es el eje a lo largo de la barra. | ||
| - | El momento cinético respecto al centro será, para una distribución continua | + | El momento cinético respecto al centro de la barra 8que es también su centro de masas) será, para una distribución continua |
<center><math>\mathbf{L}_C=\int \mathrm{d}m\,\mathbf{r}\times\mathbf{v}</math></center> | <center><math>\mathbf{L}_C=\int \mathrm{d}m\,\mathbf{r}\times\mathbf{v}</math></center> | ||
Revisión de 21:24 1 mar 2010
Contenido |
1 Enunciado
Una barra homogénea de masa m y longitud h gira en torno a un eje perpendicular a ella y que pasa
por su centro, con velocidad angular uniforme  .
.
- Calcula el momento angular de la barra respecto a su punto central.
- Ahora el eje de giro pasa por uno de sus extremos. Calcula el momento angular de la barra en este caso, respecto a un punto del eje de giro.
- En la situación anterior, la longitud de la barra se multiplica por dos, mientras que su masa permanece constante. ¿Cómo cambia la velocidad angular? ¿Y si se divide por dos?
2 Rotación en torno al centro
Tomamos un sistema de ejes fijos en el cual el origen de coordenadas es el centro de la barra, el eje Z es el eje instantáneo de rotación y X es el eje a lo largo de la barra.
El momento cinético respecto al centro de la barra 8que es también su centro de masas) será, para una distribución continua
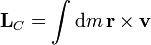
Para calcular esta integral identificamos los puntos de la barra por su coordenada x definida en el intervalo






