Fasor
De Laplace
(→Derivación e integración de fasores) |
(→Velocidad en un MAS) |
||
| Línea 54: | Línea 54: | ||
Si derivamos la expresión fasorial obtenemos la velocidad instantánea de una partícula en un MAS | Si derivamos la expresión fasorial obtenemos la velocidad instantánea de una partícula en un MAS | ||
| - | v = \dot{x}=\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\mathrm{Re}\left(\tilde{x}\mathrm{e}^{\mathrm{j}\omega t}\right)\right) | + | <center><math>v = \dot{x}=\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\mathrm{Re}\left(\tilde{x}\mathrm{e}^{\mathrm{j}\omega t}\right)\right)</math></center> |
| + | |||
| + | La derivada de una parte real es la parte real de la derivada, y <math>\tilde{x}</math> es una cantidad constante, por lo que | ||
| + | |||
| + | <center><math>v = \mathrm{Re}\left(\tilde{x}\frac{\mathrm{d}\ }{\mathrm{d}t}\left(ºmathrm{e}^{\mathrm{j}\omega t}\right)\right) = \mathrm{Re}\left(\mathrm{j}\omega\tilde{x}\mathrm{e}^{\mathrm{j}\omega t}\right)</math></center> | ||
Revisión de 10:56 10 feb 2010
Contenido |
1 Fórmula de Euler
Existe una forma expresar el movimiento armónico simple. La fórmula de Euler establece una relación entre la exponencial de un número imaginario y las funciones trigonométricas
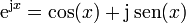
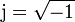
o, equivalentemente,
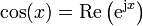
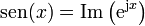
2 Vectores rotatorios
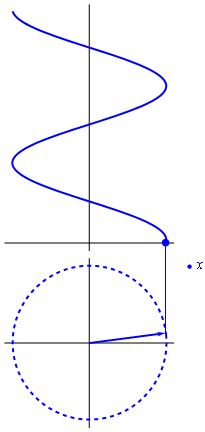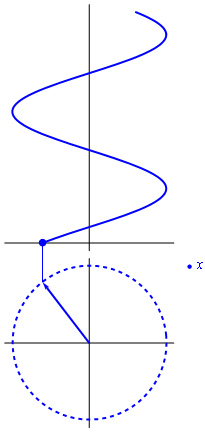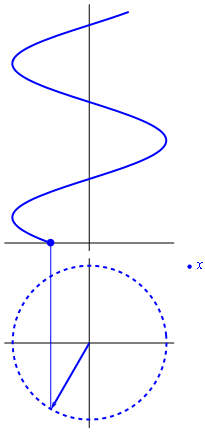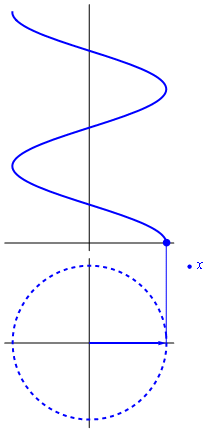
Si consideramos que el exponente en la fórmula de Euler es proporcional al tiempo, el resultado es un vector rotatorio en el plano complejo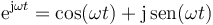
La parte real de este número complejo rotatorio, esto es, su proyección sobre el eje de abscisas, representa una oscilación cosenoidal. La parte imaginaria oscila igualmente, pero como un seno, esto es, desfasada un cuarto de periodo.
3 Amplitudes complejas (fasores)
La solución general del movimiento armónico simple, en función de las condiciones iniciales, es
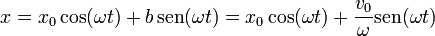
y, en función de la amplitud y la fase
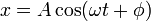


Aplicando la fórmula de Euler a la expresión anterior

donde
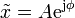
es la llamada amplitud compleja o fasor de la variable x. El movimiento armónico simple se puede ver entonces como la proyección sobre el eje real de un vector que gira en el plano complejo y cuyo valor en el instante t = 0 es la amplitud compleja 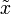 .
.
Se define entonces, en general, la amplitud compleja o fasor 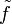 de una cantidad oscilante f(t) como aquel número complejo constante que cuando se multiplica por ejωt y se halla la parte real del producto, resulta la cantidad f(t).
de una cantidad oscilante f(t) como aquel número complejo constante que cuando se multiplica por ejωt y se halla la parte real del producto, resulta la cantidad f(t).
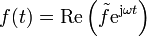
Este número complejo tiene por módulo la amplitud de las oscilaciones y por argumento la constante de fase
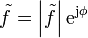
Aplicando de nuevo la fórmula de Euler obtenemos la parte real y la imaginaria del fasor de la posición

esto es, la amplitud compleja queda completamente determinada por las condiciones iniciales del movimiento.
4 Derivación e integración de fasores
La gran ventaja de la definición de los fasores es que simplifican enormemente las derivadas e integrales.
4.1 Velocidad en un MAS
Si derivamos la expresión fasorial obtenemos la velocidad instantánea de una partícula en un MAS
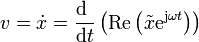
La derivada de una parte real es la parte real de la derivada, y 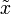 es una cantidad constante, por lo que
es una cantidad constante, por lo que