Fasor
De Laplace
(Diferencias entre revisiones)
Antonio (Discusión | contribuciones)
(Nueva página: ==Introducción== Existe una forma expresar el movimiento armónico simple. La fórmula de Euler establece una relación entre la exponencial de un número imaginario y las funcio...)
Edición más nueva →
(Nueva página: ==Introducción== Existe una forma expresar el movimiento armónico simple. La fórmula de Euler establece una relación entre la exponencial de un número imaginario y las funcio...)
Edición más nueva →
Revisión de 18:19 9 feb 2010
Introducción
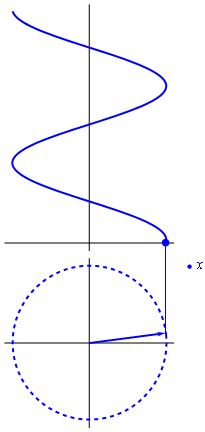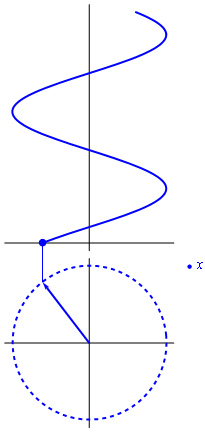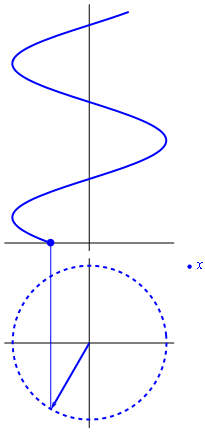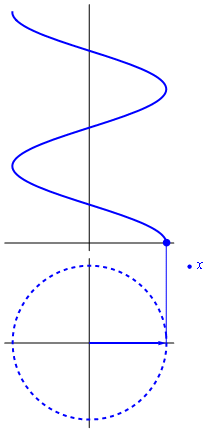
Existe una forma expresar el movimiento armónico simple. La fórmula de Euler establece una relación entre la exponencial de un número imaginario y las funciones trigonométricas
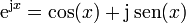
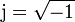
o, equivalentemente,
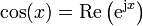
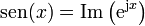
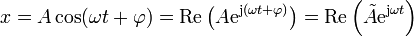
donde
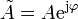
es la llamada amplitud compleja o fasor de la variable x. Es un número complejo cuyo módulo es la amplitud del movimiento y cuyo argumento es la constante de fase.
Aplicando de nuevo la fórmula de Euler obtenemos la parte real y la imaginaria del fasor
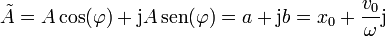
esto es, la amplitud compleja queda completamente determinada por las condiciones iniciales. Vemos que el vector de componentes a y b que definimos anteriormente no es más que la representación del fasor en el plano complejo.