Ecuaciones de Maxwell
De Laplace
(→En forma integral) |
(→En forma integral) |
||
| Línea 17: | Línea 17: | ||
* <math>\cdot\mathbf{n}</math>: El vector <math>\mathbf{n}</math> es el vector unitario normal a la superficie cerrada <math>\partial\tau</math> y que apunta hacia el exterior. El producto escalar por este vector indica que el integrando es sólo la componente del campo eléctrico perpendicular a la superficie <math>E_n = \mathbf{E}\cdot\mathbf{n}</math> | * <math>\cdot\mathbf{n}</math>: El vector <math>\mathbf{n}</math> es el vector unitario normal a la superficie cerrada <math>\partial\tau</math> y que apunta hacia el exterior. El producto escalar por este vector indica que el integrando es sólo la componente del campo eléctrico perpendicular a la superficie <math>E_n = \mathbf{E}\cdot\mathbf{n}</math> | ||
| - | * <math>\mathrm{d}S</math>: Es un diferencial de área sobre <math>\partial\tau</math>. Normalmente se combina con el vector <math>\mathbf{n}</math> para dar el [[vector superficie|diferencial de superficie]] <math>\mathrm{d}\mathbf{S}= | + | * <math>\mathrm{d}S</math>: Es un diferencial de área sobre <math>\partial\tau</math>. Normalmente se combina con el vector <math>\mathbf{n}</math> para dar el [[vector superficie|diferencial de superficie]] <math>\mathrm{d}\mathbf{S}=\mathbf{n}\,\mathrm{d}S</math>. |
Por tanto, el primer miembro nos dice que tomemos una superficie cerrada, que hallemos el la componente normal (exterior) del campo eléctrico en los puntos de dicha superficie, que multipliquemos esta componente por el área del elemento de superficie, y sumemos para toda ella. | Por tanto, el primer miembro nos dice que tomemos una superficie cerrada, que hallemos el la componente normal (exterior) del campo eléctrico en los puntos de dicha superficie, que multipliquemos esta componente por el área del elemento de superficie, y sumemos para toda ella. | ||
última version al 12:14 9 feb 2010
Contenido |
1 Introducción
2 Ley de Gauss
2.1 En forma integral
La ley de Gauss para el campo eléctrico se expresa, en forma integral

Analizando cada uno de los símbolos que aparecen en esta expresión
-
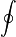 : El símbolo de integral con un círculo quiere decir que se trata de una integral sobre una superficie cerrada.
: El símbolo de integral con un círculo quiere decir que se trata de una integral sobre una superficie cerrada.
-
 : representa que dicha superficie cerrada es la frontera (
: representa que dicha superficie cerrada es la frontera (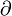 ) de un volumen τ.
) de un volumen τ.
-
 : el campo eléctrico en los puntos de la superficie. Este campo es el total, producido por todas las fuentes que haya en el universo. El que esté en negrita indica que es un vector, también podría ponerse
: el campo eléctrico en los puntos de la superficie. Este campo es el total, producido por todas las fuentes que haya en el universo. El que esté en negrita indica que es un vector, también podría ponerse 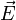 .
.
-
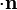 : El vector
: El vector  es el vector unitario normal a la superficie cerrada
es el vector unitario normal a la superficie cerrada  y que apunta hacia el exterior. El producto escalar por este vector indica que el integrando es sólo la componente del campo eléctrico perpendicular a la superficie
y que apunta hacia el exterior. El producto escalar por este vector indica que el integrando es sólo la componente del campo eléctrico perpendicular a la superficie 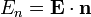
- dS: Es un diferencial de área sobre
 . Normalmente se combina con el vector
. Normalmente se combina con el vector  para dar el diferencial de superficie
para dar el diferencial de superficie 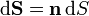 .
.
Por tanto, el primer miembro nos dice que tomemos una superficie cerrada, que hallemos el la componente normal (exterior) del campo eléctrico en los puntos de dicha superficie, que multipliquemos esta componente por el área del elemento de superficie, y sumemos para toda ella.
El segundo miembro tiene solo dos términos
-
 : una constante universal denominada la permitividad del vacío.
: una constante universal denominada la permitividad del vacío.
- Qint: la carga encerrada, esto es, la carga neta contenida dentro de la superficie
 .
.
Por tanto, la ley de Gauss nos dice que el flujo del campo eléctrico producido por todas las cargas del universo a través de una superficie cerrada es proporcional a la carga no a toda la carga que produce el campo, sino solo a la carga encerrada por dicha superficie. La carga exterior a la superficie, aunque sí contribuye al campo, no contribuye al flujo (o, con más precisión, la contribución al flujo del campo de las cargas exteriores es nula).
2.2 En forma diferencial
2.3 Condición de salto
3 Ley de Faraday
3.1 En forma integral
3.2 En forma diferencial
3.3 Condición de salto
4 Ley de Gauss para el campo magnético
4.1 En forma integral
4.2 En forma diferencial
4.3 Condición de salto
5 Ley de Ampère-Maxwell
5.1 En forma integral
5.2 En forma diferencial
5.3 Condición de salto
6 Tabla de las ecuaciones
| Nombre | Ecuación | Condición |
|---|---|---|
| Ley de Gauss | 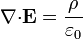
| ![\mathbf{n}{\cdot}[\mathbf{E}]= \frac{\sigma_s}{\varepsilon_0}](/wiki/images/math/f/d/2/fd21bf106305546f7c65555e79d17ca2.png)
|
| Ley de Faraday | 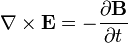
| ![\mathbf{n}\times[\mathbf{E}]=\mathbf{0}](/wiki/images/math/6/d/9/6d9a6f945a9f8273282ed8720257a0ba.png)
|
| Ley de Gauss para el campo magnético | 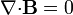
| ![\mathbf{n}{\cdot}[\mathbf{B}]=0\,](/wiki/images/math/a/5/c/a5cb589bc054897456fda0273d15e8c8.png)
|
| Ley de Ampère-Maxwell | 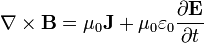
| ![\mathbf{n}\times[\mathbf{B}] = \mu_0\mathbf{K}](/wiki/images/math/a/3/9/a396b6021f5168cdc941f9d6d3353db1.png)
|
A su vez, se denominan ecuaciones homogéneas a la ley de Fraday a la de Gauss para el campo magnético, e inhomogéneas (porque aparecen las fuentes) a la de Gauss y la de Ampère-Maxwell.
Por último, dado que estas ecuaciones incluyen derivadas respecto al tiempo, deben ser suplementadas con las condiciones iniciales correspondientes.





