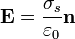Consecuencias del equilibrio electrostático
De Laplace
(→Equipotencialidad) |
(→Densidad volumétrica nula) |
||
| Línea 54: | Línea 54: | ||
==Densidad volumétrica nula== | ==Densidad volumétrica nula== | ||
| + | La ley de Gauss en forma diferencial nos permite calcular la densidad de carga, conocido el campo eléctrico. Para cualquier punto del interior del material conductor | ||
| + | |||
| + | <center><math>\rho(\mathbf{r})=\varepsilon_0\nabla\cdot\mathbf{E}=\varepsilon_0\nabla\cdot\mathbf{0}=0</math></center> | ||
| + | |||
| + | La densidad volumétrica de carga es nula en todos los puntos del interior del material conductor en equilibrio. | ||
| + | |||
| + | Este resultado se puede interpretar físicamente de la siguiente forma: si hubiera una densidad de carga neta, necesariamente habría campo en los alrededores (pues las cargas son manantiales y sumideros de campo eléctrico), lo que rompería la situación de equilibrio electrostático. | ||
| + | |||
| + | Por supuesto, cuando decimos que la densidad de carga de volumen es nula, no estamos diciendo que no haya carga alguna en el material. Un material conductor no es más que un conjunto de átomos, cada uno de los cuales se compone de numerosos protones y electrones, cada uno con su carga eléctrica. Por tanto, en cada elemento de volumen <math>\Delta\tau</math> existen miles de millones de cargas individuales. Lo que se anula es la carga <math>neta</math> en cada elemento de volumen, de acuerdo con la definición de densidad de carga | ||
| + | |||
| + | <center><math>\rho(\mathbf{r})=\frac{1}{\Delta\tau}\sum_{q_i\in\tau}q_i</math></center> | ||
| + | |||
| + | De hecho, cuando se dice, con cierta ligereza, que “todas las cargas se van a la superficie” | ||
| + | |||
==Densidad superficial no nula== | ==Densidad superficial no nula== | ||
==Líneas de campo prohibidas== | ==Líneas de campo prohibidas== | ||
Revisión de 11:11 10 ene 2010
Contenido |
1 Introducción
Como consecuencia de la condición de equilibrio electrostático
- El campo eléctrico es nulo en el material conductor
- El material conductor es equipotencial.
- No hay densidad de carga de volumen en el material.
- Toda la carga está almacenada en las superficies del conductor.
- No hay líneas de campo que vayan de un conductor a él mismo.
- El campo justo fuera del conductor es perpendicular a la superficie.
- El campo justo fuera del condductor es de la forma
Veamos cada una de estas propiedades por separado.
2 Anulación del campo
La condición de equilibrio electrostático requiere que las cargas se encuentren reposo en el material conductor. Esto es, no se mueven, pese a que podrían hacerlo (pues un material conductor permite el desplazamiento de carga por su interior).
Si las cargas se encuentran en equilibrio, la fuerza sobre cada una de ellas debe ser nula
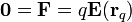
Puesto que esto tiene que ser cierto para cada carga en cualquier punto del interior del material conductor, ello implica que
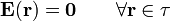
siendo τ el volumen de material conductor.
Esta es la propiedad básica que caracteriza a los conductores en equilibrio electrostático. Todas las demás que veremos se deducen de ella.
Hay que insistir que esta propiedad se cumple para un conductor en equilibrio. Si el conductor no está en equilibrio, porque está circulando una corriente por su interior, entonces no es cierto que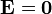 
. No hay que pensar que, por el simple hecho de ser conductor, ya el campo se anula en un material. La misma salvedad al resto de las propiedades que siguen.
3 Equipotencialidad
Supongamos dos puntos, A y B, en el material conductor. La diferencia de potencial entre estos dos puntos es
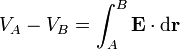
donde la integral se calcula a lo largo de una curva arbitraria que conecte A y B. Puesto que podemos elegir la que queramos, podemos tomar una que recorra exclusivamente el interior del material conductor, en el cual el campo eléctrico es nulo. En ese caso
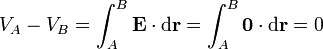
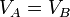
Por tanto, todo el volumen del conductor es equipotencial
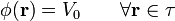
Esta condición se aplica, en particular, a los puntos de la superficie del conductor, 
:
La superficie de un conductor en equilibrio es una superficie equipotencial.
Esta propiedad se cumple siempre que exista ese camino que conecte los dos puntos. Por ejemplo, si tenemos dos bloques metálicos unidos por un fino cable y el sistema está en equilibrio, los dos bloques están al mismo potencial, porque podemos hallar un camino, que pasa por el cable, para cualesquiera dos puntos de los bloques. Si el cable de conexión no está presente, los potenciales de los dos conductores, aunque estén en equilibrio, no tienen por qué ser iguales. En cada uno será una constante, pero estas constantes pueden ser diferentes.
Por supuesto, esta propiedad no se cumple si el conductor no está en equilibrio. Si hay una corriente fluyendo por el material habrá puntos que estén a un potencial y otros a otro, aunque sean puntos del mismo conductor.
4 Densidad volumétrica nula
La ley de Gauss en forma diferencial nos permite calcular la densidad de carga, conocido el campo eléctrico. Para cualquier punto del interior del material conductor
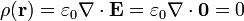
La densidad volumétrica de carga es nula en todos los puntos del interior del material conductor en equilibrio.
Este resultado se puede interpretar físicamente de la siguiente forma: si hubiera una densidad de carga neta, necesariamente habría campo en los alrededores (pues las cargas son manantiales y sumideros de campo eléctrico), lo que rompería la situación de equilibrio electrostático.
Por supuesto, cuando decimos que la densidad de carga de volumen es nula, no estamos diciendo que no haya carga alguna en el material. Un material conductor no es más que un conjunto de átomos, cada uno de los cuales se compone de numerosos protones y electrones, cada uno con su carga eléctrica. Por tanto, en cada elemento de volumen Δτ existen miles de millones de cargas individuales. Lo que se anula es la carga neta en cada elemento de volumen, de acuerdo con la definición de densidad de carga
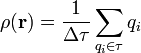
De hecho, cuando se dice, con cierta ligereza, que “todas las cargas se van a la superficie”
5 Densidad superficial no nula
6 Líneas de campo prohibidas
7 Ortogonalidad a la superficie
8 Proporcionalidad a σs
