Sistemas de partículas
De Laplace
(Diferencias entre revisiones)
(Nueva página: ==Definición de sistema de partículas== ==Propiedades de un sistema de partículas== ===Masa total=== ===Centro de masas=== ===Cantidad de movimiento=== ===Momento angular (o cinét...) |
(→Definición de sistema de partículas) |
||
| Línea 1: | Línea 1: | ||
==Definición de sistema de partículas== | ==Definición de sistema de partículas== | ||
| + | En mecánica consideramos un sistema de partículas como un conjunto de <math>N</math> puntos materiales que se mueven por separado, si bien interactúan entre sí y están sometidos a fuerzas externas. | ||
| + | |||
| + | Cada una de las partículas del sistema posee una masa propia, <math>m_i</math>, siendo <math>i=1,\ldots,N</math> un índice que sirve para etiquetar individualmente cada una de las partículas. la partícula <math>i</math> está caracterizada por una posición <math>\mathbf{r}_i</math> y una velocidad <math>\mathbf{v}_i</math>. Esta posición y esta velocidad evolucionan de acurdo con las leyes de la dinámica | ||
| + | |||
| + | <center><math>\frac{\mathrm{d}\mathbf{r}_i}{\mathrm{d}t}=\mathbf{v}_i</math>{{qquad}}{{qquad}}<math>m_i \frac{\mathrm{d}\mathbf{v}_i}{\mathrm{d}t} = \mathbf{F}_i</math>{{qquad}}{{qquad}}<math>i=1,\ldts,N</math></center> | ||
| + | |||
| + | siendo <math>\mathbf{F}_i</math> la resultante de las fuerzas que actúan sobre la partícula <math>i</math> | ||
| + | |||
==Propiedades de un sistema de partículas== | ==Propiedades de un sistema de partículas== | ||
===Masa total=== | ===Masa total=== | ||
Revisión de 21:04 12 dic 2009
Contenido |
1 Definición de sistema de partículas
En mecánica consideramos un sistema de partículas como un conjunto de N puntos materiales que se mueven por separado, si bien interactúan entre sí y están sometidos a fuerzas externas.
Cada una de las partículas del sistema posee una masa propia, mi, siendo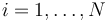 
un índice que sirve para etiquetar individualmente cada una de las partículas. la partícula i está caracterizada por una posición 
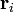y una velocidad 
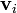. Esta posición y esta velocidad evolucionan de acurdo con las leyes de la dinámica
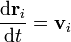
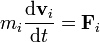No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): i=1,\ldts,N
siendo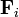 
la resultante de las fuerzas que actúan sobre la partícula i
