Trabajo para cuatro cargas en un cuadrado
De Laplace
(→Trabajo para reunir las cuatro cargas) |
(→Proceso de reunión) |
||
| Línea 25: | Línea 25: | ||
<center><math>W_3= q_3\left(\phi_1(\mathbf{r}_3)+\phi_2(\mathbf{r}_3)\right) = \frac{ | <center><math>W_3= q_3\left(\phi_1(\mathbf{r}_3)+\phi_2(\mathbf{r}_3)\right) = \frac{ | ||
| - | -q}{4\pi\varepsilon_0}\left(\frac{q}{a}+\frac{q}{\sqrt{2}a}\right)=-\frac{q^ | + | -q}{4\pi\varepsilon_0}\left(\frac{q}{a}+\frac{q}{\sqrt{2}a}\right)=-\frac{q^2}{4\pi\varepsilon_0a}\left(1+\frac{1}{\sqrt{2}}\right)</math></center> |
* La cuarta carga es atraída por las dos primeras y repelida por la tercera | * La cuarta carga es atraída por las dos primeras y repelida por la tercera | ||
| Línea 33: | Línea 33: | ||
Sumando las cuatro contribuciones hallamos el trabajo total | Sumando las cuatro contribuciones hallamos el trabajo total | ||
| + | |||
| + | <center><math>W=\sum_{i=1}^4 W_i=\frac{q^2}{4\pi\varepsilon_0a}\left(0+1-\left(1+\frac{\sqrt{2}}\right)-\frac{1}{\sqrt{2}}\right)=-\frac{\sqrt{2}q^2}{4\pi\varepsilon_0a}</math></center> | ||
==Trabajo para permutar cargas opuestas== | ==Trabajo para permutar cargas opuestas== | ||
==Trabajo para permutar cargas contiguas== | ==Trabajo para permutar cargas contiguas== | ||
[[Categoría:Problemas de electrostática en el vacío]] | [[Categoría:Problemas de electrostática en el vacío]] | ||
Revisión de 12:20 15 nov 2009
Contenido |
1 Enunciado
Cuatro cargas puntuales se sitúan en los vértices de un cuadrado de lado a. Dos de ellas, situadas en vértices adyacentes, son de valor + q, mientras que las otras dos valen − q.
Calcule el trabajo para reunir esta distribución de cargas.
Suponga que una de las cargas positivas se intercambia con la negativa situada en el vértice opuesto, ¿qué trabajo hay que realizar para esta operación?
Si la carga positiva se permuta con la negativa situada en el vértice vecino, ¿cuál será en este caso, el trabajo realizado?
2 Trabajo para reunir las cuatro cargas
Podemos calcular el trabajo de dos formas equivalentes: hallar el trabajo a partir de un proceso arbitrario que las lleva del infinito a su posición final, o bien a partir de la variación en la energía almacenada.
2.1 Proceso de reunión
Si colocamos las cargas una a una en sus posiciones finales, trayéndolas desde el infinito, los sucesivos trabajos individuales son:
- Para traer la primera carga positiva, el trabajo es nulo:
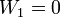
- Para traer la segunda carga positiva debemos vencer la repulsión de la primera
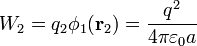
- La primera carga negativa es atraída por las dos previas, por lo que el trabajo correspondiente es negativo
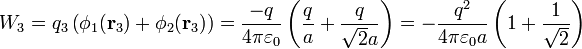
- La cuarta carga es atraída por las dos primeras y repelida por la tercera
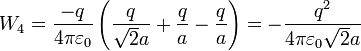
Sumando las cuatro contribuciones hallamos el trabajo total





