Derivada direccional
De Laplace
(→Derivadas parciales) |
|||
| Línea 19: | Línea 19: | ||
Un caso particular importante de derivada direccional lo dan las ''derivadas parciales''. Supongamos que queremos calcular la derivada direccional en la dirección marcada por <math>\mathbf{u}_x\,</math>. La aplicación del límite nos da | Un caso particular importante de derivada direccional lo dan las ''derivadas parciales''. Supongamos que queremos calcular la derivada direccional en la dirección marcada por <math>\mathbf{u}_x\,</math>. La aplicación del límite nos da | ||
| - | <center><math>\frac{\partial\phi}{\partial | + | <center><math>\frac{\partial\phi}{\partial x} = \lim_{h\to 0}\frac{\phi(\mathbf{r}_0+h\bu{x})-\phi(\mathbf{r}_0)}{h}</math></center> |
| + | |||
| + | pero, si consideramos <math>\phi\,</math> como función de las tres coordenadas <math>x\,</math>, <math>y\,</math> y <math>z\,</math>, moverse en la dirección de <math>\mathbf{u}_x\,</math> equivale a variar la coordenada <math>x\,</math>, manteniendo las otras dos constantes, esto es | ||
| + | |||
| + | <center><math>\frac{\partial\phi}{\partial x} = \lim_{h\to 0}\frac{\phi(x_0+h,y_0,z_0})-\phi(x_0,y_0,z_0)}{h}</math></center> | ||
| + | |||
| + | esto es, resulta la derivada ordinaria de la función <math>\phi\,</math> con respecto a <math>x\,</math>, tratando a <math>y\,</math> y <math>z\,</math> como constantes. Esta es la interpretación habitual de derivada parcial. | ||
| + | |||
| + | Vemos, no obstante, que las derivadas parciales pueden entenderse como las derivadas direccionales según las direcciones paralelas a los ejes coordenados. | ||
| + | |||
==Ejemplo== | ==Ejemplo== | ||
Revisión de 15:44 18 ene 2008
Contenido |
1 Introducción
Cuando se define la derivada en una dimensión su interpretación geométrica es sencilla: la derivada de una función en punto es igual a la pendiente de la tangente a la gráfica de la función en dicho punto.
Sin embargo, no es posible intentar extender esa interpretación a campos dependientes de dos o tres coordenadas. Consideremos por ejemplo una función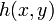 
que representa la altura de los puntos de una montaña. Si nos situamos en un punto de la ladera, ¿qué significa la "pendiente" de la montaña? Hay no una, sino infinitas pendientes, dependiendo de si miramos hacia la cima, o hacia los puntos situados a la misma altura que en el que estamos, o en cualquier dirección intermedia.
La cosa es aun más complicada para campos escalares, dependientes de las tres coordenadas, ya que en ese caso ni siquiera podemos imaginar qué significa una pendiente.
Por ello, la extensión del concepto de derivada a campos escalares debe hacerse de una forma específica. Podemos definir una derivada a lo largo de una dirección determinada, pero nada más.
2 Definición
Definimos la derivada direccional de un campo escalar 
en un punto 
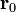según una dirección marcada por el vector unitario 
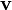, como el límite
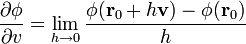
La interpretación de este límite es sencilla. Partimos de un punto 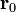y queremos determinar la pendiente en la dirección marcada por 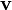. Para ello, nos desplazamos una pequeña distancia 
, con lo que acabamos en el punto 
. medimos el incremento . Este incremento, dividido por distancia recorrida , nos da la pendiente media. Si ahora tomamos el límite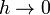 
llegamos a la derivada direccional.
3 Derivadas parciales
Un caso particular importante de derivada direccional lo dan las derivadas parciales. Supongamos que queremos calcular la derivada direccional en la dirección marcada por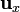 
. La aplicación del límite nos da
pero, si consideramos como función de las tres coordenadas 
, 
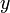y 
, moverse en la dirección de 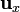equivale a variar la coordenada , manteniendo las otras dos constantes, esto es
esto es, resulta la derivada ordinaria de la función con respecto a , tratando a 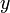y como constantes. Esta es la interpretación habitual de derivada parcial.
Vemos, no obstante, que las derivadas parciales pueden entenderse como las derivadas direccionales según las direcciones paralelas a los ejes coordenados.
