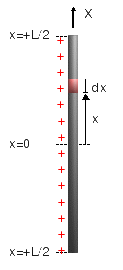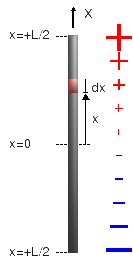Ejemplos de densidades de carga
De Laplace
(→Hilo circular con densidad de carga uniforme) |
(→Esfera cargada uniformemente) |
||
| Línea 122: | Línea 122: | ||
Como la densidad de carga es uniforme la carga total es el producto de | Como la densidad de carga es uniforme la carga total es el producto de | ||
<math>\lambda_0 </math> y la longitud del anillo. | <math>\lambda_0 </math> y la longitud del anillo. | ||
| + | |||
| + | === Disco cargada uniformemente === | ||
=== Esfera cargada uniformemente === | === Esfera cargada uniformemente === | ||
Revisión de 11:12 20 may 2009
Contenido |
1 Enunciado
Calcule la carga eléctrica total en cada uno de estos sistemas
- Un hilo de longitud L con densidad lineal de carga uniforme λ0.
- Un hilo de longitud L con densidad lineal de carga λ(x) = Ax (x = 0 corresponde al punto medio).
- Un hilo circular de radio R con densidad lineal de carga uniforme λ0.
- Un disco de radio R con densidad superficial de carga uniforme σ0.
- Una esfera de radio R con densidad volumétrica de carga uniforme ρ0.
2 Solución
2.1 Hilo recto con densidad de carga uniforme
El hilo se supone sin grosor. Por tanto, basta una coordenada para describir las posiciones a lo largo de él. Como se indica en el dibujo, si escogemos el eje X a lo largo del hilo, y el origen x = 0 en el centro del hilo, los puntos del hilo vienen descritos por los valores de la coordenada x
![x\in\left[-\frac{L}{2},+\frac{L}{2}\right]](/wiki/images/math/3/c/5/3c539103f57c24ca4b7f480657232ce9.png)
Si escogemos un elemento de línea de coordenada x y longitud dc, su carga es
dq = λ(x)dx = λ0dx
En este caso la densidad lineal de carga es uniforme, λ(x) = λ0.
Para obtener la carga total del hilo hay que sumar la carga de todos los elementos de línea que podemos considerar a lo largo de él, para todos los posibles valores de x. Esto da la integral
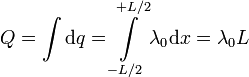
En este caso de distribución uniforme de carga la carga total es simplemente el producto de la densidad lineal por la longitud del hilo. La distribución de carga a lo largo del hilo está indicada en la figura, suponiendo que λ0 es positiva. Todos los elementos de línea tienen la misma carga.
2.2 Hilo recto con densidad de carga no uniforme
La geometría es similar a la del caso anterior. La diferencia es que ahora la densidad de carga no es uniforme. Se anula en el punto medio del hilo y es positiva en la parte superior y negativa en la inferior, alcanzando un máximo en valor absoluto en los extremos. Para un elemento de línea dx la carga es
dq = λ(x)dx = Axdx
En este caso la carga total es
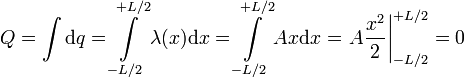
La carga total es cero. Como puede verse en el dibujo, la distribución de carga es simétrica respecto al punto medio, positiva por arriba y negativa por abajo, de modo que la carga neta se anula.
Este problema muestra como dar la carga total de un objeto no proporciona toda la información de la distribución de carga que tiene. Así, este hilo tiene carga total cero, pero va a producir un campo eléctrico, pues hay separación de cargas positivas y negativas en él.
2.3 Hilo circular con densidad de carga uniforme
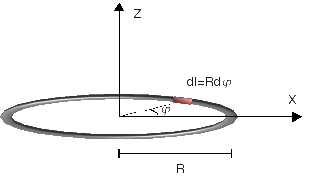
De nuevo tenemos una distribución de carga filiforme, es decir, basta una coordenada para describir la posición de un punto a lo largo del hilo. La diferencia con el caso anterior es que no vamos a escoger como coordenada la longitud recorrida sobre el hilo, sino el ángulo φ indicado en la figura. Como la densidad de carga es uniforme, cualquier punto puede escogerse como φ = 0. Para describir todos los puntos del anillo el ángulo debe recorrer los valores
![\phi\in[0,2\pi]](/wiki/images/math/2/8/1/2810c622d09f4cece4e0b5e23450ea1b.png)
La longitud de un elemento de línea del anillo es
dl = Rdφ
Y la carga de ese elemento de línea es
dq = λ(φ)dl = λ0Rdφ
Hemos usado que la densidad lineal de carga tiene el mismo valor para todos los valores de φ.
Para obtener la carga total del anillo integramos para todos los valores de φ

Como la densidad de carga es uniforme la carga total es el producto de λ0 y la longitud del anillo.