Representación de campos vectoriales
De Laplace
(Diferencias entre revisiones)
(→Campos bidimensionales) |
(→Campos bidimensionales) |
||
| Línea 2: | Línea 2: | ||
Un campo vectorial bidimensional es uno que depende solo de dos coordenadas y además posee sólo dos componentes | Un campo vectorial bidimensional es uno que depende solo de dos coordenadas y además posee sólo dos componentes | ||
| - | <center><math>\mathbf{A} = A_x(x,y)\mathbf{u}_x + A_y(x,y)mathbf{u}_y</math></center> | + | <center><math>\mathbf{A} = A_x(x,y)\mathbf{u}_x + A_y(x,y)\mathbf{u}_y</math></center> |
Para este tipo de campos es posible hacer representaciones más o menos ilustrativas, a partir de un ''array'' de flechas, que representan el valor del vector en una malla rectangular de puntos. | Para este tipo de campos es posible hacer representaciones más o menos ilustrativas, a partir de un ''array'' de flechas, que representan el valor del vector en una malla rectangular de puntos. | ||
Revisión de 10:59 2 dic 2007
1 Campos bidimensionales
Un campo vectorial bidimensional es uno que depende solo de dos coordenadas y además posee sólo dos componentes
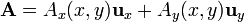
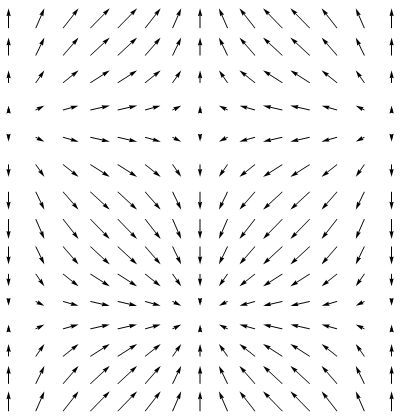
Para este tipo de campos es posible hacer representaciones más o menos ilustrativas, a partir de un array de flechas, que representan el valor del vector en una malla rectangular de puntos.
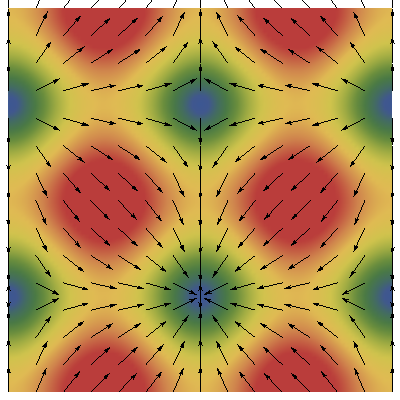
Cuando el módulo varía mucho de un punto a otro, puede ser más ilustrativo combinar la representación de un campo escalar (el módulo del campo vectorial) con un array de vectores unitarios que indican la dirección.
2 Campos tridimensionales
3 Enlaces
- Siguiente: Líneas de campo
- Anterior:





