Teorema de Carnot
De Laplace
(Nueva página: ==Introducción== ==Enunciado== ==Demostración== ==Corolario== ==Ejemplos== ==Refrigeradores y bombas de calor== Categoría:Segundo Principio) |
|||
| Línea 1: | Línea 1: | ||
==Introducción== | ==Introducción== | ||
| - | + | El ''teorema de Carnot'' es un enunciado alternativo del Segundo Principio de la termodinámica, que se formula a partir de la comparación entre máquinas reversibles y máquinas irreversibles como: | |
| + | |||
| + | <blockquote>''El rendimiento de una máquina térmica M que opere entre dos focos no puede ser superior que el de una máquina reversible que opere entre los mismos focos''</blockquote> | ||
| + | |||
| + | <center><math>\eta_M \leq \eta_\mathrm{rev}\,</math></center> | ||
| + | |||
| + | <blockquote>''cumpliéndose la igualdad si la máquina M es también reversible y la desigualdad si es irreversible.''</blockquote> | ||
| + | |||
| + | Puede demostrarse que el teorema de Carnot es equivalente al enunciado de Kelvin-Planck, aunque está formulado de una forma mucho más concreta que éste. El de Kelvin-Planck simplemente nos dice que no existe la máquina perfecta con rendimiento del 100%. El teorema de Carnot nos dice además que existe un máximo para ese rendimiento e incluso establece cómo hallar ese máximo. Basta con calcular el rendimiento de una máquina reversible que actúe entre las dos temperaturas indicadas. | ||
| + | |||
| + | Máquinas reversibles puede haber muchas con diferentes soportes (solo gas, agua y vapor, materiales magnéticos,…) por lo que puede resultar sorprendente que el rendimiento de todas ellas sea el mismo si trabajan entre las mismas temperaturas. | ||
| + | |||
==Demostración== | ==Demostración== | ||
==Corolario== | ==Corolario== | ||
==Ejemplos== | ==Ejemplos== | ||
==Refrigeradores y bombas de calor== | ==Refrigeradores y bombas de calor== | ||
| + | |||
| + | La aplicación del teorema de Carnot a un refrigerador establece que el COP máximo lo da un refrigerador que opere según un ciclo reversible, como el de Carnot. Este valor máximo es | ||
| + | |||
| + | <center><math>\mathrm{COP}_R=\frac{|Q_f|}{|Q_c|-|Q_f|} \leq \mathrm{COP}_\mathrm{max}=\frac{T_f}{T_c-T_f}</math></center> | ||
| + | |||
| + | Para un frigorífico que mantiene los productos a 5°C en una habitación a 22°C este valor máximo es 16.4. Un frigorífico real posee un COP en torno a 4. | ||
| + | |||
| + | Para una bomba de calor, el COP máximo lo da también una bomba reversible, siendo su valor máximo | ||
| + | |||
| + | <center><math>\mathrm{COP}_\mathrm{BC} = \frac{|Q_c|}{|Q_c|-|Q_f|}\leq \mathrm{COP}_\mathrm{max}=\frac{T_c}{T_c-T_f}</math></center> | ||
| + | |||
| + | Una bomba de calor que mantiene una habitación a 22°C mientras el exterior está a 5°C tiene un coeficiente de desempeño máximo de 17.4 (uno más que para el frigorífico). | ||
[[Categoría:Segundo Principio]] | [[Categoría:Segundo Principio]] | ||
Revisión de 22:08 19 may 2010
Contenido |
1 Introducción
El teorema de Carnot es un enunciado alternativo del Segundo Principio de la termodinámica, que se formula a partir de la comparación entre máquinas reversibles y máquinas irreversibles como:
El rendimiento de una máquina térmica M que opere entre dos focos no puede ser superior que el de una máquina reversible que opere entre los mismos focos
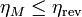
cumpliéndose la igualdad si la máquina M es también reversible y la desigualdad si es irreversible.
Puede demostrarse que el teorema de Carnot es equivalente al enunciado de Kelvin-Planck, aunque está formulado de una forma mucho más concreta que éste. El de Kelvin-Planck simplemente nos dice que no existe la máquina perfecta con rendimiento del 100%. El teorema de Carnot nos dice además que existe un máximo para ese rendimiento e incluso establece cómo hallar ese máximo. Basta con calcular el rendimiento de una máquina reversible que actúe entre las dos temperaturas indicadas.
Máquinas reversibles puede haber muchas con diferentes soportes (solo gas, agua y vapor, materiales magnéticos,…) por lo que puede resultar sorprendente que el rendimiento de todas ellas sea el mismo si trabajan entre las mismas temperaturas.
2 Demostración
3 Corolario
4 Ejemplos
5 Refrigeradores y bombas de calor
La aplicación del teorema de Carnot a un refrigerador establece que el COP máximo lo da un refrigerador que opere según un ciclo reversible, como el de Carnot. Este valor máximo es
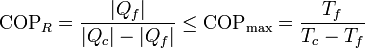
Para un frigorífico que mantiene los productos a 5°C en una habitación a 22°C este valor máximo es 16.4. Un frigorífico real posee un COP en torno a 4.
Para una bomba de calor, el COP máximo lo da también una bomba reversible, siendo su valor máximo
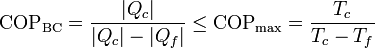
Una bomba de calor que mantiene una habitación a 22°C mientras el exterior está a 5°C tiene un coeficiente de desempeño máximo de 17.4 (uno más que para el frigorífico).





