Problemas de Gas Ideal
De Laplace
(Diferencias entre revisiones)
(→Ecuación de estado) |
(→Pistón oscilante) |
||
| Línea 10: | Línea 10: | ||
== Pistón oscilante == | == Pistón oscilante == | ||
| + | |||
| + | Un cilindro de 2.4 m de altura se llena con 0.1 moles de un gas ideal a una | ||
| + | temperatura y presión normales. El cilindro se cierra entonces con un pistón | ||
| + | de masa 1.4 kg que se deja caer hasta alcanzar el equilibrio. | ||
| + | |||
| + | #Determine la altura <math>h_0</math> del pistón suponiendo que la temperatura del gas no varía en la compresión. | ||
| + | #Suponga que el pistón se empuja ligeramente hacia abajo más allá de la posición de equilibrio y luego se libera. Suponiendo que la temperatura del gas permanece constante y que el rozamiento del pistón es despreciable, demuestre que el pistón describe un movimiento armónico simple y determine su frecuencia. | ||
| + | |||
| + | [[Pistón oscilante|'''Solución''']] | ||
== Trabajo en distintos procesos == | == Trabajo en distintos procesos == | ||
Revisión de 12:56 16 abr 2009
1 Ecuación de estado
Utilizando la ecuación de estado de los gases ideales, responda a las siguientes preguntas
- ¿Que volumen ocupa un mol de gas en condiciones estándar?
- ¿Cuantas moléculas hay en
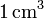de gas ideal a una temperatura de 300 K y a una presión de 1 atm?
¿Y si la presión es de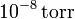 
?
2 Pistón oscilante
Un cilindro de 2.4 m de altura se llena con 0.1 moles de un gas ideal a una temperatura y presión normales. El cilindro se cierra entonces con un pistón de masa 1.4 kg que se deja caer hasta alcanzar el equilibrio.
- Determine la altura h0 del pistón suponiendo que la temperatura del gas no varía en la compresión.
- Suponga que el pistón se empuja ligeramente hacia abajo más allá de la posición de equilibrio y luego se libera. Suponiendo que la temperatura del gas permanece constante y que el rozamiento del pistón es despreciable, demuestre que el pistón describe un movimiento armónico simple y determine su frecuencia.
