Partícula magnética en un campo externo

De Laplace

(Diferencias entre revisiones)

Revisión de 14:17 30 mar 2009

Contenido

1 Enunciado
2 Magnetización y campo
3 Caso de un material lineal
4 Corrientes de imanación
5 Casos particulares

1 Enunciado

Supóngase que se tiene una esfera de radio $R$ un material magnético lineal (de permeabilidad $μ$ ) alrededor de la cual hay vacío. En puntos alejados de la esfera hay impuesto un campo magnético uniforme $\mathbf{B}_0$ .

Sabiendo que la magnetización que aparece en la esfera es uniforme, halle el valor de dicha magnetización, del momento dipolar inducido en la esfera, y del campo magnético en todos los puntos del espacio.
¿En qué se diferencia el resultado para un material diamagnético de uno paramagnético? ¿A qué se reducen los resultados en los casos de un paramagnético ideal ( 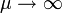$\mu\to\infty$ ) y un superconductor ( $μ = 0$ )?
Halle las corrientes de magnetización que aparecen en la esfera.
Calcule los valores numéricos para los apartados anteriores con un campo externo $B 0 = 10mT$ aplicado sobre una esfera de radio 1 cm para los siguientes materiales: oro, aluminio, hierro y un superconductor.

2 Magnetización y campo

Este problema tiene una total analogía con el correspondiente problema para dieléctricos.

La idea es que el campo externo, induce una magnetización en la esfera. Esta magnetización genera un campo, que es uniforme en el interior, y que también debe incluirse en los cálculos.

En el interior de la esfera el campo será la suma del externo y del debido a la magnetización. Este último, para una magnetización uniforme, vale

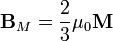
$\mathbf{B}_M=\frac{2}{3}\mu_0\mathbf{M}$

con lo que el campo total es

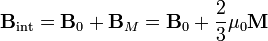
$\mathbf{B}_\mathrm{int}=\mathbf{B}_0+\mathbf{B}_M=\mathbf{B}_0+\frac{2}{3}\mu_0\mathbf{M}$

La magnetización, por su parte, es proporcional al campo total en el interior de la esfera. Aplicando que

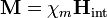
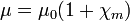
$\mathbf{M}=\chi_m\mathbf{H}_\mathrm{int}\,$ $\mu=\mu_0(1+\chi_m)\,$ $\mathbf{B}_\mathrm{int}=\mu\mathbf{H}_\mathrm{int}\,$

resulta

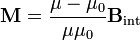
$\mathbf{M}=\frac{\mu-\mu_0}{\mu\mu_0}\mathbf{B}_\mathrm{int}$

sustituyendo en la expresión anterior, queda la ecuación para $\mathbf{B}$ .

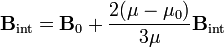
$\mathbf{B}_\mathrm{int}=\mathbf{B}_0+\frac{2(\mu-\mu_0)}{3\mu}\mathbf{B}_\mathrm{int}$

y despejando, obtenemos el campo en el interior de la esfera

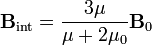
$\mathbf{B}_\mathrm{int}=\frac{3\mu}{\mu+2\mu_0}\mathbf{B}_0$

Conocido el campo tenemos la magnetización de la esfera

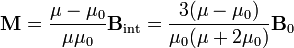
$\mathbf{M}=\frac{\mu-\mu_0}{\mu\mu_0}\mathbf{B}_\mathrm{int}=\frac{3(\mu-\mu_0)}{\mu_0(\mu+2\mu_0)}\mathbf{B}_0$

y el momento magnético de la esfera, por ser la magnetización uniforme

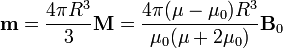
$\mathbf{m}=\frac{4\pi R^3}{3}\mathbf{M} = \frac{4\pi(\mu-\mu_0)R^3}{\mu_0(\mu+2\mu_0)}\mathbf{B}_0$

El campo magnético en el exterior de la esfera es la superposición del campo externo y del debido a un dipolo puntual en el centro de la esfera.

$\mathbf{B}_\mathrm{ext}=\mathbf{B}_0+\frac{\mu_0}{4\pi}\,\frac{3(\mathbf{m}{\cdot}\mathbf{r})\mathbf{r}-r^2\mathbf{m}}{r^5}$

3 Caso de un material lineal

4 Corrientes de imanación

5 Casos particulares

@@ Línea 22: / Línea 22: @@
 La magnetización, por su parte, es proporcional al campo total en el interior de la esfera. Aplicando que
-<math>\mathbf{M}=\chi_m\mathbf{H}_\mathrm{int}\,</math>{{qquad}}{{qquad}}<math>\mu=\mu_0(1+\chi_m)\,</math>{{qquad}}{{qquad}}<math>\mathbf{B}_\mathrm{int}=\mu\mathbf{H}_\mathrm{int}\,</math>
+<center><math>\mathbf{M}=\chi_m\mathbf{H}_\mathrm{int}\,</math>{{qquad}}{{qquad}}<math>\mu=\mu_0(1+\chi_m)\,</math>{{qquad}}{{qquad}}<math>\mathbf{B}_\mathrm{int}=\mu\mathbf{H}_\mathrm{int}\,</math>
+</center>
 resulta

Partícula magnética en un campo externo

De Laplace

Revisión de 14:17 30 mar 2009

Contenido

1 Enunciado

2 Magnetización y campo

3 Caso de un material lineal

4 Corrientes de imanación

5 Casos particulares

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES