Entrar Página Discusión Historial Go to the site toolbox

Dipolo magnético

De Laplace

(Diferencias entre revisiones)
(→Para una espira)
(→Para una espira)
Línea 95: Línea 95:
* Para una espira plana, el momento magnético tiene por módulo el producto de la corriente por el área de la porción plana delimitado por la espira, y por sentido el normal a la superficie, según la regla de la mano derecha (si la corriente es positiva; en sentido opuesto en caso contrario).
* Para una espira plana, el momento magnético tiene por módulo el producto de la corriente por el área de la porción plana delimitado por la espira, y por sentido el normal a la superficie, según la regla de la mano derecha (si la corriente es positiva; en sentido opuesto en caso contrario).
 +
 +
<center>[[Imagen:momentom1.png]]</center>
* Para una espira alabeada el vector superficie tiene por componentes las áreas de las proyecciones de la superficie sobre los planos coordenados. El momento magnético es igual a este vector multiplicado por la corriente.
* Para una espira alabeada el vector superficie tiene por componentes las áreas de las proyecciones de la superficie sobre los planos coordenados. El momento magnético es igual a este vector multiplicado por la corriente.

Revisión de 11:38 27 mar 2009

Contenido

1 Desarrollo multipolar magnético

Supongamos que tenemos una distribución de corriente estacionaria que ocupa una pequeña región del espacio y queremos hallar el campo en puntos alejados.

Cuando se dice “una pequeña región del espacio” se entiende que comparada con la distancia al punto de observación. Matemáticamente:

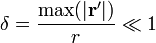
\delta=\frac{\mathrm{max}(|\mathbf{r}'|)}{r}\ll 1

Como con el campo eléctrico, la idea del desarrollo multipolar es hacer un cálculo aproximado, más sencillo que la integral exacta (la cual puede ser imposible de calcular) mediante el empleo de una serie de Taylor. Partimos de la expresión del potencial vector para el caso de una espira

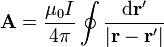
\mathbf{A}=\frac{\mu_0I}{4\pi}\oint\frac{\mathrm{d}\mathbf{r}'}{|\mathbf{r}-\mathbf{r}'|}

Aplicando el desarrollo del binomio de Newton

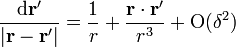
\frac{\mathrm{d}\mathbf{r}'}{|\mathbf{r}-\mathbf{r}'|}=\frac{1}{r}+\frac{\mathbf{r}\cdot\mathbf{r}'}{r^3}+\mathrm{O}(\delta^2)

resulta (de forma no trivial) la expresión aproximada para el potencial vector

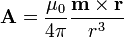
\mathbf{A}=\frac{\mu_0}{4\pi}\frac{\mathbf{m}\times\mathbf{r}}{r^3}

donde

\mathbf{m}=\frac{I}{2}\oint \mathbf{r}'\times\mathrm{d}\mathbf{r}'

es el momento magnético dipolar de la espira.

1.1 Demostración detallada

La obtención de la expresión aproximada del potencial vector no es elemental.

Para empezar hay que justificar el desarrollo de 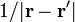1/|\mathbf{r}-\mathbf{r}'|. Para ello observamos que se puede escribir como

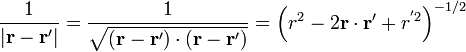
\frac{1}{|\mathbf{r}-\mathbf{r}'|}=\frac{1}{\sqrt{(\mathbf{r}-\mathbf{r}')\cdot(\mathbf{r}-\mathbf{r}')}}=\left(r^2-2\mathbf{r}\cdot\mathbf{r}'+r^{'2}\right)^{-1/2}

y sacando factor común un r2 de la raíz

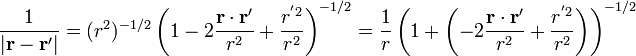
\frac{1}{|\mathbf{r}-\mathbf{r}'|}=(r^2)^{-1/2}\left(1-2\frac{\mathbf{r}\cdot\mathbf{r}'}{r^2}+\frac{r^{'2}}{r^2}\right)^{-1/2} = \frac{1}{r}\left(1+\left(-2\frac{\mathbf{r}\cdot\mathbf{r}'}{r^2}+\frac{r^{'2}}{r^2}\right)\right)^{-1/2}

Hasta aquí no hay aproximación alguna. Observamos que en el último factor tenemos 1 más algo mucho más pequeño que la unidad (pues 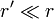r'\ll r). La fórmula general del binomio de Newton nos dice que si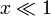 x\ll 1

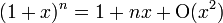
(1+x)^n = 1 + n x + \mathrm{O}(x^2)\,

Aplicando esto al resultado anterior

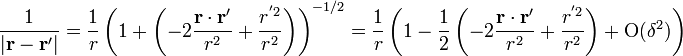
\frac{1}{|\mathbf{r}-\mathbf{r}'|} = \frac{1}{r}\left(1+\left(-2\frac{\mathbf{r}\cdot\mathbf{r}'}{r^2}+\frac{r^{'2}}{r^2}\right)\right)^{-1/2} = \frac{1}{r}\left(1-\frac{1}{2}\left(-2\frac{\mathbf{r}\cdot\mathbf{r}'}{r^2}+\frac{r^{'2}}{r^2}\right)+\mathrm{O}(\delta^2)\right)

pero de hecho, el segundo de los dos sumandos del paréntesis también es de orden δ2, por lo que podemos despreciarlo y reducir el desarrollo a

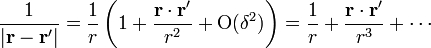
\frac{1}{|\mathbf{r}-\mathbf{r}'|} = \frac{1}{r}\left(1+\frac{\mathbf{r}\cdot\mathbf{r}'}{r^2}+\mathrm{O}(\delta^2)\right)= \frac{1}{r}+\frac{\mathbf{r}\cdot\mathbf{r}'}{r^3}+\cdots

El segundo paso es sustituir esto en la expresión del potencial vector. Nos queda

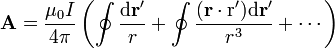
\mathbf{A}=\frac{\mu_0I}{4\pi}\left(\oint\frac{\mathrm{d}\mathbf{r}'}{r}+\oint\frac{(\mathbf{r}\cdot\mathrm{r}')\mathrm{d}\mathbf{r}'}{r^3}+\cdots\right)

Estas integrales son sobre la variable 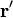\mathbf{r}', así que \mathbf{r} es una constante en ellas y puede ser extraído en la medida de lo posible

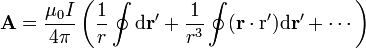
\mathbf{A}=\frac{\mu_0I}{4\pi}\left(\frac{1}{r}\oint\mathrm{d}\mathbf{r}'+\frac{1}{r^3}\oint(\mathbf{r}\cdot\mathrm{r}')\mathrm{d}\mathbf{r}'+\cdots\right)

La primera de estas dos integrales es el desplazamiento neto al recorrer una curva cerrada, por lo que se anula identicamente,

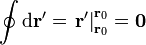
\oint \mathrm{d}\mathbf{r}'=\left.\mathbf{r}'\right|_{\mathbf{r}_0}^{\mathbf{r}_0}=\mathbf{0}

Lo que nos dice este resultado, de nuevo, es que el campo magnético de corrientes estacionarias, no posee término monopolar, esto es, que el campo de corrientes no equivale al campo de cargas magnéticas (monopolos).

El segundo término no se puede integrar de forma inmediata. Para conseguir extraer \mathbf{r} de la integral podemos usar el teorema vectorial, generalización del teorema de Stokes

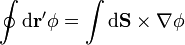
\oint \mathrm{d}\mathbf{r}' \phi = \int \mathrm{d}\mathbf{S}\times\nabla\phi

que, en nuestro caso da

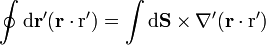
\oint \mathrm{d}\mathbf{r}'(\mathbf{r}\cdot\mathrm{r}') = \int \mathrm{d}\mathbf{S}\times\nabla'(\mathbf{r}\cdot\mathrm{r}')

pero, como se puede demostrar

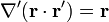
\nabla'(\mathbf{r}\cdot\mathbf{r}')=\mathbf{r}

por lo que la integral se convierte en

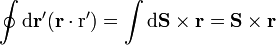
\oint \mathrm{d}\mathbf{r}'(\mathbf{r}\cdot\mathrm{r}') = \int \mathrm{d}\mathbf{S}\times\mathbf{r}=\mathbf{S}\times\mathbf{r}

y, aplicación la expresión del vector superficie

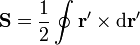
\mathbf{S}=\frac{1}{2}\oint \mathbf{r}'\times \mathrm{d}\mathbf{r}'

nos queda finalmente

\mathbf{A}=\frac{\mu_0}{4\pi}\,\frac{\mathrm{m}\times\mathbf{r}}{r^3}+\cdots        \mathbf{m}=I\mathbf{S}=\frac{I}{2}\oint \mathbf{r}'\times \mathrm{d}\mathbf{r}'

2 Momento dipolar magnético

2.1 Para una espira

El momento magnético dipolar de una espira cerrada por la cual circula una corriente I viene dado por la expresión

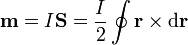
\mathbf{m}=I\mathbf{S}=\frac{I}{2}\oint \mathbf{r}\times\mathrm{d}\mathbf{r}

Aquí 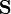\mathbf{S} es el vector superficie, por lo que

  • Para una espira plana, el momento magnético tiene por módulo el producto de la corriente por el área de la porción plana delimitado por la espira, y por sentido el normal a la superficie, según la regla de la mano derecha (si la corriente es positiva; en sentido opuesto en caso contrario).
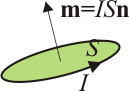
Imagen:momentom1.png
  • Para una espira alabeada el vector superficie tiene por componentes las áreas de las proyecciones de la superficie sobre los planos coordenados. El momento magnético es igual a este vector multiplicado por la corriente.

2.1.1 Ejemplos

2.1.1.1 Espira rectangular
2.1.1.2 Espira circular
2.1.1.3 Espira tridimensional

2.2 Para una distribución de corriente

3 Campo magnético de un dipolo

4 Acción de un campo externo sobre un dipolo

4.1 Fuerza

4.2 Par y momento

4.3 Energía

Obtenido de "http://tesla.us.es/wiki/index.php/Dipolo_magn%C3%A9tico"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace