Campo magnético de una espira circular

De Laplace

(Diferencias entre revisiones)

Revisión de 13:37 20 mar 2009

Contenido

1 Enunciado
2 Solución

1 Enunciado

Supongamos una espira circular por la cual circula una corriente $I$ . Se trata de hallar el campo magnético en los puntos del eje de la espira (para el resto del espacio no existe expresión analítica sencilla)

2 Solución

2.1 Planteamiento

Aplicamos la ley de Biot y Savart

$\mathbf{B}\left(\mathbf{r}\right) = \frac{\mu _0I}{4\pi}\int\mathrm{d}\mathbf{r}'\times\frac{\left(\mathbf{r} - \mathbf{r}'\right)}{\left|\mathbf{r} - \mathbf{r}'\right|^3}$

Tomamos como eje z el de la espira, de forma que

$\mathbf{r} = z\mathbf{u}_z\,$ $\mathbf{r}' = R\left(\cos\varphi'\,\mathbf{u}_x + \,\mathrm{sen}\,\varphi'\,\mathbf{u}_y\right)$ $\mathrm{d}\mathbf{r}' = R\left(-\,\mathrm{sen}\,\varphi'\,\mathbf{u}_x + \cos\varphi'\,\mathbf{u}_y \right)\mathrm{d}\varphi '$

$\mathbf{r} - \mathbf{r}' = - R\cos\varphi'\,\mathbf{u}_x - R\,\mathrm{sen},\varphi'\,\mathbf{u}_y + z\mathbf{u}_z$ $\left|\mathbf{r} - \mathbf{r}'\right| = \sqrt{R^2 + z^2}$

Hallando el producto vectorial y extrayendo los factores constantes:

$\mathbf{B}(z) = \frac{\mu _0IR}{4\pi\left(R^2 + z^2\right)^{3/2}}\left(\mathbf{u}_xz\int_0^{2\pi}\!\!\!\! \cos\varphi'\,\mathrm{d}\varphi' + \mathbf{u}_yz\int_0^{2\pi}\!\!\!\!\mathrm{sen}\,\varphi'\mathrm{d}\varphi' + \mathbf{u}_zR\int_0^{2\pi}\!\!\!\!\mathrm{d}\varphi'\right)$

Las integrales para $B x$ y $B y$ se anulan, lo que se puede explicar como que el campo horizontal de un segmento de espira se anula con el del diametralmente opuesto.

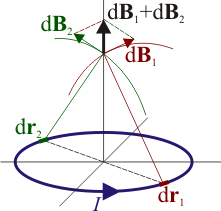
Integrando la componente $z$ queda el campo

$\mathbf{B}_z=\frac{\mu_0IR^2}{2(R^2+z^2)^{3/2}}\mathbf{u}_z$

2.2 Análisis de los resultados

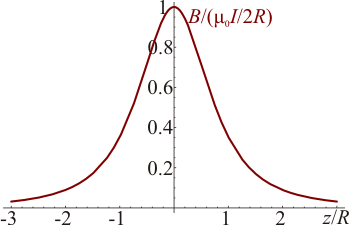
Este campo va en la dirección del eje y su gráfica es una campana con un máximo en el centro.

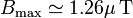El valor máximo del campo es $B_\mathrm{max}=\mu_0I/2R\,$ , que para una espira de 10 cm por la cual circule una corriente de 1 A da un campo $B_\mathrm{max} \simeq 1.26\mu\,\mathrm{T}$ .

2.3 Campo en todo el espacio

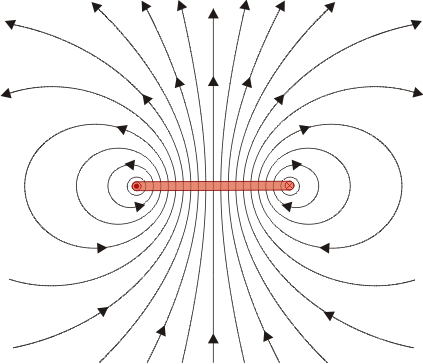
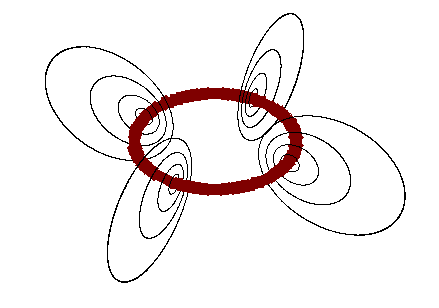
En el resto del espacio el campo se puede calcular de forma numérica o de forma analítica, resultando líneas cerradas alrededor de la espira. Las líneas están en planos 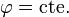$\varphi=\mathrm{cte.}$ . La distribución de líneas posee simetría acimutal.

Las líneas de campo salen por la cara superior (definida según la regla de la mano derecha) y entran por la cara inferior.

La expresión analítica del campo en todo el espacio puede calcularse a partir del potencial vector

$\mathbf{A}=\frac{\mu_0I}{4\pi}\int \frac{\mathrm{d}\mathbf{r}'}{|\mathbf{r}-\mathbf{r}'|}$

a partir del cual el campo magnético se calcula como

$\mathbf{B}=\nabla\times\mathbf{A}$

En este caso en que tenemos una corriente puramente acimutal, el potencial vector posee la misma simetría

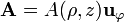
$\mathbf{A}=A(\rho,z)\mathbf{u}_\varphi$

El campo magnético resultante se encuentra contenido en planos 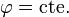$\varphi=\mathrm{cte.}$ . Hallando el rotacional en coordenadas cilíndricas,

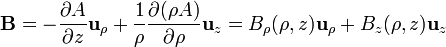
$\mathbf{B}= -\frac{\partial A}{\partial z}\mathbf{u}_\rho+\frac{1}{\rho}\frac{\partial(\rho A)}{\partial\rho}\mathbf{u}_z = B_\rho(\rho,z)\mathbf{u}_\rho+B_z(\rho,z)\mathbf{u}_z$

Una vez calculado el potencial vector, puede obtenerse la ecuación de las líneas de campo, que son solución de la ecuación diferencial

$\frac{\mathrm{d}\rho}{B_\rho}=\frac{\mathrm{d}z}{B_z}$ $\Rightarrow$ $0=B_z\,\mathrm{d}\rho-B_\rho\mathrm{d}z=\frac{1}{\rho}\left(\frac{\partial(\rho A)}{\partial \rho}\mathrm{d}\rho+\frac{\partial(\rho A)}{\partial z}\mathrm{d}z\right)$

La última expresión es una diferencial exacta. Por ello, las líneas de campo magnético vienen dadas por la ecuación

$\rho\,A(\rho,z)=\mathrm{cte.}$

Calculando la integral resulta, para el potencial vector

$\mathbf{A}=\frac{\mu_0I}{2\pi r}\left(\frac{r^2+R^2+z^2}{\sqrt{(r+R)^2+z^2}}\mathrm{K}\left(\frac{4 rR}{(r+R)^2+z^2}\right)-\sqrt{(r+R)^2+z^2}\,\mathrm{E}\left(\frac{4Rr}{(r+R)^2+z^2}\right)\right)\mathbf{u}_\varphi$

siendo $E(m)$ y $K(m)$ las integrales elípticas completas de primera y segunda especie:

$\mathrm{E}(m)=\int_0^{\pi/2}\!\!\sqrt{1-m\,\mathrm{sen}^2(t)}\,\mathrm{d}t$ $\mathrm{K}(m)=\int_0^{\pi/2}\!\!\frac{\mathrm{d}t}{\sqrt{1-m\,\mathrm{sen}^2(t)}}$

2.4 El límite dipolar

@@ Línea 31: / Línea 31: @@
 Este campo va en la dirección del eje y su gráfica es una campana con un máximo en el centro.
-El valor máximo del campo es <math>B_\mathrm{max}=\mu_0I/2R</math>, que para una espira de 10&thinsp;cm por la cual circule una corriente de 1&thinsp;A da un campo <math>B_\mathrm{max} \simeq 1.26\mu\,\mathrm{T}</math>.
+El valor máximo del campo es <math>B_\mathrm{max}=\mu_0I/2R\,</math>, que para una espira de 10&thinsp;cm por la cual circule una corriente de 1&thinsp;A da un campo <math>B_\mathrm{max} \simeq 1.26\mu\,\mathrm{T}</math>.
 ===Campo en todo el espacio===

Campo magnético de una espira circular

De Laplace

Revisión de 13:37 20 mar 2009

Contenido

1 Enunciado

2 Solución

2.1 Planteamiento

2.2 Análisis de los resultados

2.3 Campo en todo el espacio

2.4 El límite dipolar

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES