Segunda Prueba de Control 2020/21 (G.I.E.R.M.)

De Laplace

Revisión de 16:52 27 ene 2021 (ver código fuente) Pedro (Discusión | contribuciones) (→Barra deslizando en cuenco semiesférico) ← Edición más antigua		Revisión de 16:57 27 ene 2021 (ver código fuente) Pedro (Discusión | contribuciones) (→Masa con cuerda enrollándose en un disco) Edición más nueva →
Línea 21:		Línea 21:
	#La velocidad <math>\vec{v}^{\,O}_{21}</math>.		#La velocidad <math>\vec{v}^{\,O}_{21}</math>.
-	==[[ Masa con cuerda enrollándose en un disco, Enero 2021 (G.I.E.R.M.)|  Masa con cuerda enrollándose en un disco ]]==	+	==[[ Masa con cuerda desenrollándose de un disco, Enero 2021 (G.I.E.R.M.)|  Masa con cuerda desenrollándose de un disco ]]==
		+	[[Archivo:F1GIERM-masaMuelleDisco-enunciado.png|right]]
		+	Una masa <math>m</math> desliza sobre una superficie horizontal lisa. Está conectada a un muelle de constante
		+	elástica <math>k=mg/R</math> y longitud natural <math>l_0=R</math>. Por el otro lado tira de ella una cuerda sin masa que
		+	puede enrollarse y desenrollarse en un disco de masa <math>m</math> y radio <math>R</math>. El disco puede rotar alrededor de
		+	un eje perpendicular a él que pasa por su centro. El sistema está sometido a la
		+	acción de la gravedad. En el instante inicial la masa se encuentra en el punto <math>B</math>. Tanto la masa como
		+	el disco están en reposo en ese instante inicial. Durante todo el movimiento la cuerda permanece tensa.
		+	El momento de inercia de un disco de masa <math>M</math> y radio <math>R</math>
		+	respecto a un eje perpendicular a él que pasa por su centro es <math>I=MR^2/2</math>.
		+
		+	#Calcula la rapidez de la masa cuando llega al punto <math>O</math>
		+	#¿Qué trabajo ha hecho la cuerda sobre la masa durante su movimiento?
		+	#Si el contacto entre la masa y la superficie horizontal es rugoso con coeficiente de rozamiento dinámico <math>\mu</math>, calcula la velocidad de la masa en el punto <math>O</math>
		+	#¿Qué condición debe cumplir <math>\mu</math> para que la masa no llegue al punto <math>O</math>?

---

Revisión de 16:57 27 ene 2021

1 Partícula subiendo por arco de circunferencia con muelle

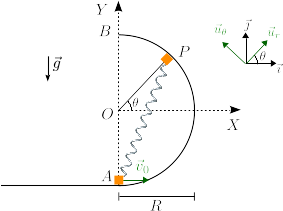
partícula de masa m se desliza por una superficie horizontal lisa con velocidad . En el punto A

empieza a deslizar por un semiaro de radio R como se indica en la figura. El contacto entre la partícula y el semiaro es liso. Durante su movimiento sobre el aro está sometida, además de la gravedad, a la fuerza de un muelle de constante elástica k = mg / R y longitud natural nula. El muelle está anclado en el punto A. En la figura se muestran los vectores de la base polar junto con la base cartesiana.

1. Esribe el vector y la aceleración de la partícula en la base polar.
2. Encuentra la expresión que da la energía mecánica de la partícula para un punto $P$ arbitrario del semiaro es (tomando como referencia de energía potencial gravitatoria nula la altura del eje $X$)
3. ¿Cuál es el valor mínimo de $v_0$ para que la partícula llegue al punto $B$?
4. Escribe la ecuación de movimiento.

2 Barra deslizando en cuenco semiesférico

Una barra de longitud L (sólido "2") desliza en un cuenco de radio R (sólido "1"). El punto A de la barra desliza sobre la circunferencia del cuenco y el punto de la barra que en cada instante está en contacto con la esquina (punto C en la figura) desliza sobre esa esquina. En el instante indicado en la figura el punto A de la barra está en el punto mas bajo del cuenco. El punto A realiza un movimiento circular uniforme sobre el cuenco con rapidez constante v₀. Calcula las siguientes magnitudes

1. La posición del C.I.R. del movimiento {21}.
2. La reducción cinemática del movimiento.
3. La velocidad .

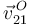3 Masa con cuerda desenrollándose de un disco

Una masa m desliza sobre una superficie horizontal lisa. Está conectada a un muelle de constante elástica k = mg / R y longitud natural l₀ = R. Por el otro lado tira de ella una cuerda sin masa que puede enrollarse y desenrollarse en un disco de masa m y radio R. El disco puede rotar alrededor de un eje perpendicular a él que pasa por su centro. El sistema está sometido a la acción de la gravedad. En el instante inicial la masa se encuentra en el punto B. Tanto la masa como el disco están en reposo en ese instante inicial. Durante todo el movimiento la cuerda permanece tensa. El momento de inercia de un disco de masa M y radio R respecto a un eje perpendicular a él que pasa por su centro es I = MR² / 2.

1. Calcula la rapidez de la masa cuando llega al punto O
2. ¿Qué trabajo ha hecho la cuerda sobre la masa durante su movimiento?
3. Si el contacto entre la masa y la superficie horizontal es rugoso con coeficiente de rozamiento dinámico μ, calcula la velocidad de la masa en el punto O
4. ¿Qué condición debe cumplir μ para que la masa no llegue al punto O?