Segunda Prueba de Control 2020/21 (G.I.E.R.M.)

De Laplace

Revisión de 16:22 27 ene 2021 (ver código fuente) Pedro (Discusión | contribuciones) (→Partícula subiendo por arco de circunferencia con muelle) ← Edición más antigua		Revisión de 16:27 27 ene 2021 (ver código fuente) Pedro (Discusión | contribuciones) (→Barra deslizando en cuenco semiesférico) Edición más nueva →
Línea 11:		Línea 11:
	==[[ Barra deslizando en cuenco semiesférico, Enero 2021 (G.I.E.R.M.)|  Barra deslizando en cuenco semiesférico ]]==		==[[ Barra deslizando en cuenco semiesférico, Enero 2021 (G.I.E.R.M.)|  Barra deslizando en cuenco semiesférico ]]==
		+	[[Archivo:F1GIERM-barraCuenco-enunciado.png|right]]
		+	Una barra de longitud <math>L</math> (sólido "2") desliza en un cuenco de radio <math>R</math> (sólido "1"). El punto <math>A</math> de
		+	la barra desliza sobre la circunferencia del cuenco y el punto de la barra que en cada instante está en contacto
		+	con la esquina (punto <math>C</math> en la figura) desliza sobre esa esquina. En el instante indicado en la figura
		+	el punto <math>A</math> de la barra está en el punto mas bajo del cuenco. El punto <math>A</math> realiza un movimiento circular
		+	uniforme sobre el cuenco con rapidez constante <math>v_0</math>. Calcula las siguientes magnitudes
		+	#La posición del C.I.R. del movimiento {21}.
		+	#La reducción cinemática del movimiento.
		+	#La velocidad <math>\vec{v}^{\,O}_{21}</math>.

---

Revisión de 16:27 27 ene 2021

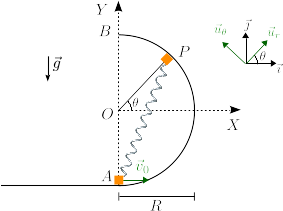
1 Partícula subiendo por arco de circunferencia con muelle

partícula de masa m se desliza por una superficie horizontal lisa con velocidad . En el punto A

empieza a deslizar por un semiaro de radio R como se indica en la figura. El contacto entre la partícula y el semiaro es liso. Durante su movimiento sobre el aro está sometida, además de la gravedad, a la fuerza de un muelle de constante elástica k = mg / R y longitud natural nula. El muelle está anclado en el punto A. En la figura se muestran los vectores de la base polar junto con la base cartesiana.

1. Esribe el vector y la aceleración de la partícula en la base polar.
2. Encuentra la expresión que da la energía mecánica de la partícula para un punto $P$ arbitrario del semiaro es (tomando como referencia de energía potencial gravitatoria nula la altura del eje $X$)
3. ¿Cuál es el valor mínimo de $v_0$ para que la partícula llegue al punto $B$?
4. Escribe la ecuación de movimiento.

2 Barra deslizando en cuenco semiesférico

Una barra de longitud L (sólido "2") desliza en un cuenco de radio R (sólido "1"). El punto A de la barra desliza sobre la circunferencia del cuenco y el punto de la barra que en cada instante está en contacto con la esquina (punto C en la figura) desliza sobre esa esquina. En el instante indicado en la figura el punto A de la barra está en el punto mas bajo del cuenco. El punto A realiza un movimiento circular uniforme sobre el cuenco con rapidez constante v₀. Calcula las siguientes magnitudes

1. La posición del C.I.R. del movimiento {21}.
2. La reducción cinemática del movimiento.
3. La velocidad .
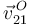