Varilla en eje giratorio (CMR)
De Laplace
(Página creada con '==Enunciado== Una varilla “3” está articulada en el punto <math>b\vec{\jmath}_2</math> de un eje <math>{OY}_2</math>. La varilla gira con velocidad angular <math>\Omega\vec…') |
|||
| Línea 6: | Línea 6: | ||
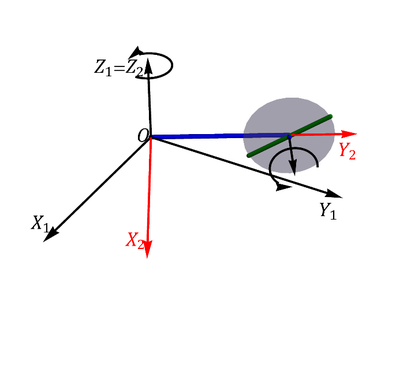
<center>[[Archivo:varilla-eje-giratorio.png|400px]]</center> | <center>[[Archivo:varilla-eje-giratorio.png|400px]]</center> | ||
==Clasificación del movimiento== | ==Clasificación del movimiento== | ||
| + | Para caracterizar el movimiento necesitamos la velocidad angular del sólido y la velocidad de un punto. | ||
| + | |||
| + | La velocidad angular la obtenemos por la ley de composición | ||
| + | <center><math>\vec{\omega}_{31}=\vec{\omega}_{32}+\vec{\omega}_{21}=\Omega\vec{\imath}_2+\Omega\vec{k}_2</math></center> | ||
| + | |||
| + | Para la velocidad de un punto, el más simple es el centro de la varilla, por tratarse de una articulación | ||
| + | |||
| + | <center><math>\vec{v}^G_{31}=\overbrace{\vec{v}^G_{32}}^{=\vec{0}}+\vec{v}^G_{21}</math></center> | ||
| + | |||
| + | A su vez, la velocidad de G en el movimiento {21} corresponde a una rotación en torno al eje <math>{OZ}_1</math> | ||
| + | |||
| + | <center><math>\vec{v}^G_{21}=\overbrace{\vec{v}^O_{21}}^{=\vec{0}}+\vec{\omega}_{21}\times\overrightarrow{OG}=\Omega\vec{k}_2\times(b\vec{\jmath}_2)=-\Omega b\vec{\imath}_2</math></center> | ||
| + | |||
| + | La reducción cinemática en G es entonces | ||
| + | |||
| + | <center><math>\left\{\vec{\omega}_{31},\vec{v}^G_{31}\right\}=\left\{\Omega\vec{\imath}_2+\Omega\vec{k}_2,-\Omega b\vec{\imath}_2\right\}</math></center> | ||
| + | |||
| + | La velocidad angular no es nula, por lo que el estado no es de reposo ni de traslación. | ||
| + | |||
| + | Si calculamos el producto escalar de las dos velocidades | ||
| + | |||
| + | <center><math>\vec{v}^G_{31}\cdot\vec{\omega}_{31}=-\Omega^2 b\neq 0</math></center> | ||
| + | |||
| + | Por tanto el movimiento es helicoidal, siendo la velocidad de deslizamiento | ||
| + | |||
| + | <center><math>v_d=\frac{\vec{v}^G_{31}\cdot\vec{\omega}_{31}}{|\vec{\omega}_{31}|}=-\frac{\Omega b}{\sqrt{2}}</math></center> | ||
| + | |||
==Ecuación del EIRMD== | ==Ecuación del EIRMD== | ||
| + | El EIRMD lleva la dirección de la velocidad angular y pasa por el punto de posición respecto a G | ||
==Aceleración angular== | ==Aceleración angular== | ||
Revisión de 13:51 1 dic 2020
Contenido |
1 Enunciado
Una varilla “3” está articulada en el punto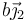 
de un eje OY2. La varilla gira con velocidad angular 
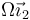(Ω=cte.) alrededor de su articulación. El eje OY2 gira a su vez con velocidad angular 
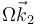respecto a un eje OZ1 de un sistema exterior fijo.
- ¿Qué tipo de movimiento es el {31}, que realiza la varilla “3” respecto al sistema exterior fijo “1” (helicoidal, rotación,…)?
- ¿Cuál es la ecuación del Eje Instantáneo de Rotación (y Mínimo Deslizamiento, en su caso), del movimiento {31}?
- ¿Cuánto vale la aceleración angular del movimiento {31}?
2 Clasificación del movimiento
Para caracterizar el movimiento necesitamos la velocidad angular del sólido y la velocidad de un punto.
La velocidad angular la obtenemos por la ley de composición
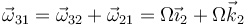
Para la velocidad de un punto, el más simple es el centro de la varilla, por tratarse de una articulación
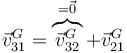
A su vez, la velocidad de G en el movimiento {21} corresponde a una rotación en torno al eje OZ1
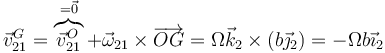
La reducción cinemática en G es entonces
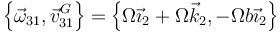
La velocidad angular no es nula, por lo que el estado no es de reposo ni de traslación.
Si calculamos el producto escalar de las dos velocidades
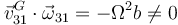
Por tanto el movimiento es helicoidal, siendo la velocidad de deslizamiento
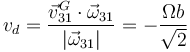
3 Ecuación del EIRMD
El EIRMD lleva la dirección de la velocidad angular y pasa por el punto de posición respecto a G
