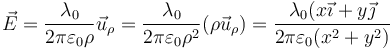Campo de un hilo infinito (GIOI)
De Laplace
(→Por integración directa) |
(→Por la ley de Gauss) |
||
| Línea 33: | Línea 33: | ||
==Por la ley de Gauss== | ==Por la ley de Gauss== | ||
| + | |||
| + | [[Categoría:Problemas de electrostática en el vacío (GIOI)]] | ||
Revisión de 10:41 14 feb 2020
1 Enunciado
A partir del resultado del problema “Campo de un segmento”, halle el campo eléctrico creado por un hilo rectilíneo infinitamente largo cargado con una densidad homogénea λ0.
Este campo puede también hallarse mediante la ley de Gauss. ¿Cómo se llega en ese caso al resultado?
2 Por integración directa
Podemos calcular el campo de un hilo infinito a partir del de un segmento. Según se ve en el problema ***, el resultado es
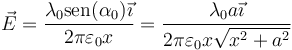
siendo α el “ángulo de elevación” del extremo del segmento.
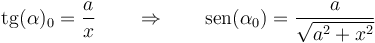
Si consideramos el límite en que la longitud de éste se hace infinita, en términos del ángulo de elevación α0 equivale a hacer
Esta expresión está particularizada para el caso de que el punto donde medimos el campo esté situado sobre el eje OX. La generalización a un punto arbitrio es inmediata.
Para un punto cualquiera, sustituimos x por la distancia al eje OZ (o, aun más en general, la línea donde se halla el hilo de carga). Empleando coordenadas cilíndricas, equivale sustituir x por ρ = (x2 + y2)1 / 2.
Además debemos dar la dirección del campo. En el caso del eje OX, 
es el unitario en el sentido de x creciente, esto es, el que se aleja en línea recta del eje OX. La generalización a cualquier punto consiste en sustituir por el unitario radial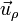 
.
Por tanto, la expresión del campo creado por un hilo cargado uniformemente es, en cualquier punto del espacio,
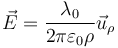
Podemos expresar este resultado en la base cartesiana como
