Problemas de electrostática en el vacío (GIOI)
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Carga total de una distribución== Calcule la carga total de las siguientes distribuciones de carga: * {{Nivel|1}} ''N'' cargas de valor ''q'' situadas en los vértices de un …') |
|||
| Línea 8: | Línea 8: | ||
* {{Nivel|2}} Una esfera maciza de radio <math>2R</math> con una densidad de carga dependiente de la distancia al centro como <math>\rho(r) = A(R-r)</math> (<math>r < 2R</math>). | * {{Nivel|2}} Una esfera maciza de radio <math>2R</math> con una densidad de carga dependiente de la distancia al centro como <math>\rho(r) = A(R-r)</math> (<math>r < 2R</math>). | ||
[[Carga total de una distribución (GIOI)|Solución]] | [[Carga total de una distribución (GIOI)|Solución]] | ||
| + | |||
| + | ==Cargas en un triángulo equilátero== | ||
| + | {{nivel|2}} Tres cargas puntuales iguales +q se hallan en los vértices de un triángulo equilátero de lado ''b''. Calcule la fuerza eléctrica sobre cada una de ellas. | ||
| + | Suponga que se cambia una de las cargas +q por una carga –q. ¿Cuánto vale en ese caso la fuerza sobre cada una de las tres cargas? | ||
| + | Si se cambia una segunda carga +q por otra carga –q, ¿cuánto pasa a ser la fuerza sobre cada una? | ||
| + | Por último, si se sustituye la última carga +q por otra –q, ¿cuál es ahora la fuerza? | ||
| + | [[Cargas en un triángulo equilátero (GIOI)|Solución]] | ||
| + | |||
| + | ==Fuerzas y momentos sobre un par de cargas== | ||
| + | {{nivel|2}} Dos cargas <math>q_1=+q</math> y <math>q_2=-q</math> se encuentran en los extremos de una varilla que se encuentra inmersa en el campo eléctrico | ||
| + | <center><math>\vec{E}=Ay\vec{\imath}+Bx^2 \vec{\kmath}</math></center> | ||
| + | * Si los extremos de la varilla se encuentran en <math>\vec{r}_1=b\vec{\imath}</math> y <math>\vec{r}_2=-b\vec{\imath}</math>, ¿cuál es el efecto del campo sobre el sistema? | ||
| + | * Si los extremos de la varilla se encuentran en <math>\vec{r}_1=b\vec{\kmath}</math> y <math>\vec{r}_2=-b\vec{\kmath}</math>, ¿cuál es el efecto del campo sobre el sistema? | ||
| + | [[Fuerzas y momentos sobre un par de cargas (GIOI)|Solución]] | ||
Revisión de 13:54 13 feb 2020
1 Carga total de una distribución
Calcule la carga total de las siguientes distribuciones de carga:
-
N cargas de valor q situadas en los vértices de un polígono regular de N lados situado en el plano XY, con centro el origen y cuyo primer vértice se encuentra en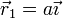 
.
- Un anillo circular de radio R con una densidad lineal de carga uniforme λ0.
-
Un anillo circular de radio R con centro el origen y situado en el plano XY, con una densidad lineal de carga λ(θ) = λ0cos(θ), siendo θ el ángulo del vector de posición con el eje OX.
- Una superficie esférica de radio a con una densidad de carga uniforme σ0, rodeada por una superficie esférica concéntrica de radio b con densidad de carga − σ0.
- Una esfera maciza de radio R con densidad de carga uniforme ρ0.
-
Una esfera maciza de radio 2R con una densidad de carga dependiente de la distancia al centro como ρ(r) = A(R − r) (r < 2R).
2 Cargas en un triángulo equilátero
Tres cargas puntuales iguales +q se hallan en los vértices de un triángulo equilátero de lado b. Calcule la fuerza eléctrica sobre cada una de ellas.
Suponga que se cambia una de las cargas +q por una carga –q. ¿Cuánto vale en ese caso la fuerza sobre cada una de las tres cargas?
Si se cambia una segunda carga +q por otra carga –q, ¿cuánto pasa a ser la fuerza sobre cada una?
Por último, si se sustituye la última carga +q por otra –q, ¿cuál es ahora la fuerza?
Solución
3 Fuerzas y momentos sobre un par de cargas
Dos cargas q1 = + q y q2 = − q se encuentran en los extremos de una varilla que se encuentra inmersa en el campo eléctrico
- Si los extremos de la varilla se encuentran en
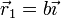y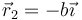 
, ¿cuál es el efecto del campo sobre el sistema?
- Si los extremos de la varilla se encuentran en No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \vec{r}_1=b\vec{\kmath}
y No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \vec{r}_2=-b\vec{\kmath}
, ¿cuál es el efecto del campo sobre el sistema? Solución
