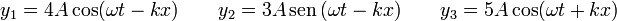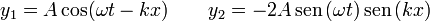Superposición de dos y tres señales

De Laplace

(Diferencias entre revisiones)

Revisión de 21:44 10 mar 2009

Contenido

1 Enunciado
2 Solución

1 Enunciado

Considere los casos de superposición siguientes

$y_1= A \cos(\omega t - kx)\qquad y_2 = A\,\mathrm{sen}\,(\omega t-kx)$
$y_1= A \cos(\omega t - kx)\qquad y_2 = A \,\mathrm{sen}\,(\omega t+kx)$
$y_1= A\cos(\omega t - kx)\qquad y_2 = -2A\,\mathrm{sen}\,(\omega t)\,\mathrm{sen}\,(k x)$
$y_1= 4A\cos(\omega t - kx)\qquad y_2 = 3A\,\mathrm{sen}\,(\omega t-kx)\qquad y_3 = 5A\cos(\omega t + kx )$

Para cada uno de los casos, determine la ecuación de la señal resultante, ¿es una onda viajera o una estacionaria?

2 Solución

2.1 Primer caso

Debemos sumar las señales

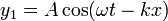
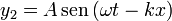
$y_1= A \cos(\omega t - kx)\,$ $y_2 = A\,\mathrm{sen}\,(\omega t-kx)$

Ambas representan señales viajando hacia la izquierda, con la misma frecuencia, por lo que su suma será otra onda viajera, cuya amplitud dependerá del desfase.

Para sumarlas de forma sencilla las escribimos ambas como cosenos. Aplicando la relación trigonométrica

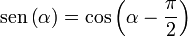
$\mathrm{sen}\left(\alpha\right)=\cos\left(\alpha-\frac{\pi}{2}\right)$

las señales quedan como

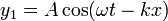
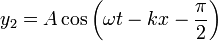
$y_1= A \cos(\omega t - kx)\,$ $y_2 = A\cos\left(\omega t-kx-\frac{\pi}{2}\right)$

Aplicando ahora la relación que transforma sumas en productos

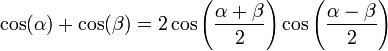
$\cos(\alpha)+\cos(\beta)=2\cos\left(\frac{\alpha+\beta}{2}\right)\cos\left(\frac{\alpha-\beta}{2}\right)$

la superposición es

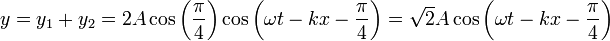
$y = y_1+y_2=2A\cos\left(\frac{\pi}{4}\right)\cos\left(\omega t-kx-\frac{\pi}{4}\right)=\sqrt{2}A \cos\left(\omega t-kx-\frac{\pi}{4}\right)$

Archivo:Seno+coseno.gif

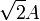Resulta una onda viajera, de amplitud $\sqrt{2}A$ (aproximadamente vez y media de la amplitud de cada onda), y con un desfase inicial de π/4.

2.2 Segundo caso

En el segundo caso

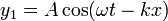
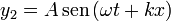
$y_1= A \cos(\omega t - kx)\,$ $y_2 = A \,\mathrm{sen}\,(\omega t+kx)$

se trata de sumar dos ondas de la misma amplitud pero que se propagan en direcciones diferentes. Por ello, su suma va a consistir en una onda estacionaria.

Como en el apartado anterior, escribimos el seno como un coseno

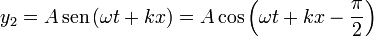
$y_2 = A \,\mathrm{sen}\,(\omega t+kx)=A\cos\left(\omega t + k x - \frac{\pi}{2}\right)$

y la transformación de sumas en productos, lo que nos da

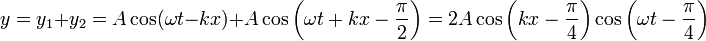
$y=y_1+y_2=A \cos(\omega t - kx)+A\cos\left(\omega t + k x - \frac{\pi}{2}\right) = 2A\cos\left(k x - \frac{\pi}{4}\right)\cos\left(\omega t - \frac{\pi}{4}\right)$

Archivo:Seno+coseno-2.gif

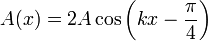
Esta es la ecuación de una onda estacionaria, con amplitud dependiente de la posición $A(x) = 2A\cos\left(k x - \frac{\pi}{4}\right)$

que alcanza el valor máximo de 2. Vemos que el efecto de introducir una fase simplemente traslada la posición de los nodos y el desfase de la oscilación de cada punto, pero produce el mismo efecto de onda estacionaria.

2.3 Tercer caso

En el tercer caso tenemos las señales

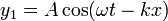
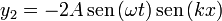
$y_1= A\cos(\omega t - kx)\,$ $y_2 = -2A\,\mathrm{sen}\,(\omega t)\,\mathrm{sen}\,(k x)$

Estas señales son respectivamente una onda viajera hacia la derecha y una onda estacionaria, por lo que no es evidente qué va a resultar de superposición.

Podemos hallarlo desarrollando el coseno de la onda viajera

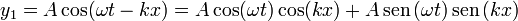
$y_1=A\cos(\omega t - kx)=A\cos(\omega t)\cos(kx)+A\,\mathrm{sen}\,(\omega t)\,\mathrm{sen}\,(kx)$

que puede interpretarse como que una onda viajera es suma de dos estacionarias (del mismo modo que una estacionaria es suma de dos viajeras). Si ahora sumamos esta forma con la segunda señal

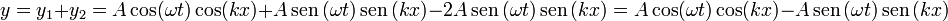
$y = y_1+y_2=A\cos(\omega t)\cos(kx)+A\,\mathrm{sen}\,(\omega t)\,\mathrm{sen}\,(kx)-2A\,\mathrm{sen}\,(\omega t)\,\mathrm{sen}\,(k x)=A\cos(\omega t)\cos(kx)-A\,\mathrm{sen}\,(\omega t)\,\mathrm{sen}\,(kx)$

y este resultado puede volverse a combinar en una onda viajera

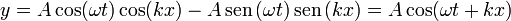
$y = A\cos(\omega t)\cos(kx)-A\,\mathrm{sen}\,(\omega t)\,\mathrm{sen}\,(kx)= A\cos(\omega t + k x)$

Nos ha resultado, por tanto, que la superposición es una onda viajera hacia la izquierda, y de la misma amplitud que la onda viajera original.

No hay que pensar que este resultado es general y que la suma de una onda viajera y una estacionaria es siempre una única onda viajera. En general resultarán dos ondas viajeras, de distinta amplitud, una en cada sentido (o, equivalentemente, una onda viajera más una estacionaria, o dos estacionarias).

2.4 Cuarto caso

$y_1= 4A\cos(\omega t - kx)\qquad y_2 = 3A\,\mathrm{sen}\,(\omega t-kx)\qquad y_3 = 5A\cos(\omega t + kx )$

@@ Línea 73: / Línea 73: @@
 y este resultado puede volverse a combinar en una onda viajera
-<center><math>y = A\cos(\omega t)\cos(kx)-A\,\mathrm{sen}\,(\omega t)\,\mathrm{sen}\,(kx)= A\cos(\omegat + k x)</math></center>
+<center><math>y = A\cos(\omega t)\cos(kx)-A\,\mathrm{sen}\,(\omega t)\,\mathrm{sen}\,(kx)= A\cos(\omega t + k x)</math></center>
-[[Imagen:seno+coseno-3.gif|left]]Nos ha resultado, por tanto, que la superposición es una onda viajera hacia la izquierda, y de la misma amplitud que la onda viajera original.
+Nos ha resultado, por tanto, que la superposición es una onda viajera hacia la izquierda, y de la misma amplitud que la onda viajera original.
 No hay que pensar que este resultado es general y que la suma de una onda viajera y una estacionaria es siempre una única onda viajera. En general resultarán dos ondas viajeras, de distinta amplitud, una en cada sentido (o, equivalentemente, una onda viajera más una estacionaria, o dos estacionarias).

Superposición de dos y tres señales

De Laplace

Revisión de 21:44 10 mar 2009

Contenido

1 Enunciado

2 Solución

2.1 Primer caso

2.2 Segundo caso

2.3 Tercer caso

2.4 Cuarto caso

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES