Primera Convocatoria Ordinaria 2018/19 (G.I.C.)
De Laplace
(→Disco subiendo escalón) |
(→Disco subiendo escalón) |
||
| Línea 23: | Línea 23: | ||
#Encuentra la expresión de las fuerzas que actúan sobre el disco en condición de equilibrio estático. ¿Para que valor de <math>h</math> cambia el sentido de la fuerza de rozamiento? | #Encuentra la expresión de las fuerzas que actúan sobre el disco en condición de equilibrio estático. ¿Para que valor de <math>h</math> cambia el sentido de la fuerza de rozamiento? | ||
#Suponiendo que <math>h=3R/2</math>, determina el valor mínimo de <math>F_0</math> para que el disco suba el escalón. | #Suponiendo que <math>h=3R/2</math>, determina el valor mínimo de <math>F_0</math> para que el disco suba el escalón. | ||
| + | |||
| + | ==[[ Ondas sísmicas (Ene. 2019 G.I.C.)| Ondas sísmicas ]]== | ||
| + | [[File:F1GIC-ondas-sismicas-enunciado.png|right]] | ||
| + | Un terremoto produce dos tipos de onda, <math>P</math> y <math>S</math>, que viajan con velocidades | ||
| + | respectivas <math>v_S=v_0</math> y <math>v_P=2v_0</math>. Un terremoto se produce en el epicentro <math>A</math> y emite los | ||
| + | dos tipos de ondas, cuyos frentes de onda se reproducen en la figura (las líneas | ||
| + | continuas son las ondas <math>P</math> y las punteadas las ondas <math>S</math>). Una estación sísmica | ||
| + | se encuentra en el punto <math>B</math>. Las ondas llegan a <math>B</math> con un intervalo de | ||
| + | tiempo entre ellas <math>\Delta t = T</math>. Determina la distancia entre el epicentro y la | ||
| + | estación sísmica | ||
última version al 13:58 31 ene 2019
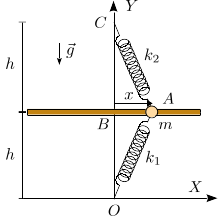
1 Partícula deslizando sobre una barra horizontal con dos muelles
Una partícula de masa m desliza por una barra fija horizontal, como se indica en la figura. La masa está conectada a dos muelles de longitud natural nula y constantes elásticas k1 = 3k y k2 = k. El contacto entre la partícula y la barra es rugoso.
- Dibuja el diagrama de cuerpo libre de la partícula. Encuentra las expresiones que dan las fuerzas que los muelles ejercen sobre la partícula.
- Calcula las fuerzas que actúan sobre la partícula cuando se encuentra en equilibrio estático.
- Si el coeficiente de rozamiento estático es μ, determina el rango de posibles posiciones de equilibrio.
- Suponemos ahora que no hay rozamiento. Encuentra la ecuación de movimiento de la partícula.
- En el instante inicial la partícula se encuentra en el puno B con velocidad v0 dirigida hacia la derecha. Encuentra la expresión x(t) que da la posición de la partícula en el tiempo.
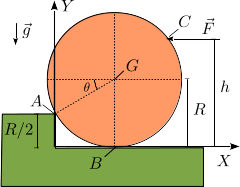
2 Disco subiendo escalón
Un disco de radio R y masa m se apoya en un escalón de altura R / 2 como se indica en la figura.
El contacto en el punto A es liso mientras que en el punto B es rugoso con coeficiente de
rozamiento estático μ. Un fuerz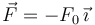a 
, con F0 > 0, se aplica en el
punto C. La gravedad actúa como se indica en la figura.
- Determina el valor del ángulo θ mostrado en la figura, así como un vector unitario con la dirección y sentido del vector
.
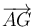- Dibuja el diagrama de fuerzas que actúan sobre el disco.
- Encuentra la expresión de las fuerzas que actúan sobre el disco en condición de equilibrio estático. ¿Para que valor de h cambia el sentido de la fuerza de rozamiento?
- Suponiendo que h = 3R / 2, determina el valor mínimo de F0 para que el disco suba el escalón.
3 Ondas sísmicas
Un terremoto produce dos tipos de onda, P y S, que viajan con velocidades respectivas vS = v0 y vP = 2v0. Un terremoto se produce en el epicentro A y emite los dos tipos de ondas, cuyos frentes de onda se reproducen en la figura (las líneas continuas son las ondas P y las punteadas las ondas S). Una estación sísmica se encuentra en el punto B. Las ondas llegan a B con un intervalo de tiempo entre ellas Δt = T. Determina la distancia entre el epicentro y la estación sísmica
