Coche impactando contra una pared
De Laplace
(Página creada con '= Enunciado = Un coche impacta contra una pared a una velocidad de 100 km/h. Estima el tiempo máximo que debe tardar el airbag en desplegarse para proteger al conductor. = Sol…') |
|||
| Línea 26: | Línea 26: | ||
<math> | <math> | ||
\dfrac{L}{2} = v_0t_d - \dfrac{1}{2}\dfrac{v_0}{t_d}\,t_d^2 | \dfrac{L}{2} = v_0t_d - \dfrac{1}{2}\dfrac{v_0}{t_d}\,t_d^2 | ||
| + | \Longrightarrow | ||
| + | t_d = \dfrac{L}{v_0}. | ||
</math> | </math> | ||
</center> | </center> | ||
| + | La longitud típica de un coche es <math>L\simeq 4\,\mathrm{m}</math>. Si <math>v_0=100\,\mathrm{km/h}</math> tenemos | ||
| + | <center> | ||
| + | <math> | ||
| + | t_d = \dfrac{4}{100}\,\dfrac{\mathrm{m}\cdot\mathrm{h}}{\mathrm{km}} | ||
| + | \,\dfrac{1\,\mathrm{km}}{10^3\,\mathrm{m}}\,\dfrac{3.6\times10^3\,\mathrm{s}}{1\,\mathrm{h}}\,\dfrac{10^3\,\mathrm{ms}}{1\,\mathrm{s}} | ||
| + | \simeq 140\,\mathrm{ms}. | ||
| + | </math> | ||
| + | </center> | ||
| + | Nuestro modelo es muy basto. Una mejora evidente es que en una colisión el coche no queda completamente aplastado. Además el centro de masas no está en el centro del coche, sino mas hacia delante, debido a la posición del motor. El valor de <math>L</math> sería mas pequeño. Los airbags reales se despliegan en un tiempo típico de 15-30 ms. | ||
| + | |||
| + | Con nuestro modelo podemos estimar también la fuerza media que recibe un ocupante del vehículo durante la colisión. | ||
| + | La aceleración es | ||
| + | <center> | ||
| + | <math> | ||
| + | a_0=\dfrac{v_0}{t_d} \simeq 190\,\mathrm{m/s^2}\simeq 20g. | ||
| + | </math> | ||
| + | </center> | ||
| + | Si escogemos <math>m=80 \,\mathrm{kg}</math> como la masa típica de una persona la fuerza que ha sufrido es | ||
| + | <center> | ||
| + | <math> | ||
| + | F=ma_0 \simeq 1.6\times10^4\,\mathrm{N}. | ||
| + | </math> | ||
| + | </center> | ||
| + | Esto es equivalente al peso de una masa de 16 Tm, aproximadamente. | ||
| + | |||
| + | |||
| + | [[Categoría:Problemas de cinemática del movimiento rectilíneo]] | ||
última version al 12:04 18 sep 2018
1 Enunciado
Un coche impacta contra una pared a una velocidad de 100 km/h. Estima el tiempo máximo que debe tardar el airbag en desplegarse para proteger al conductor.
2 Solución
Vamos a suponer que durante la colisión el coche sufre una desaceleración constante. Esto no es exactamente cierto, pero nos basta para hacer un cálculo que nos dará el orden de magnitud del tiempo que buscamos. Aplicamos entonces las expresiones del movimiento de una partícula uniformemente acelerada
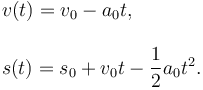
Si el coche tiene longitud L, consideramos en primera aproximación que su centro de masas, situado aproximadamente en el centro del coche, tiene que recorrer una distancia L / 2 antes de pararse. La colisión dura un tiempo td. Tenemos entonces
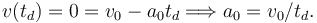
Usamos ahora la expresión que nos da la distancia recorrida (tomamos s0 = 0
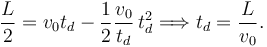
La longitud típica de un coche es 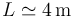 . Si
. Si 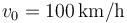 tenemos
tenemos
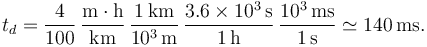
Nuestro modelo es muy basto. Una mejora evidente es que en una colisión el coche no queda completamente aplastado. Además el centro de masas no está en el centro del coche, sino mas hacia delante, debido a la posición del motor. El valor de L sería mas pequeño. Los airbags reales se despliegan en un tiempo típico de 15-30 ms.
Con nuestro modelo podemos estimar también la fuerza media que recibe un ocupante del vehículo durante la colisión. La aceleración es
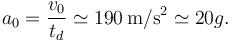
Si escogemos 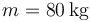 como la masa típica de una persona la fuerza que ha sufrido es
como la masa típica de una persona la fuerza que ha sufrido es
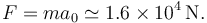
Esto es equivalente al peso de una masa de 16 Tm, aproximadamente.





