Propiedades de una onda sinusoidal
De Laplace
(Diferencias entre revisiones)
(→Solución) |
(→Frecuencia angular) |
||
| Línea 20: | Línea 20: | ||
===Frecuencia angular=== | ===Frecuencia angular=== | ||
| + | La frecuencia angular, <math>\omega</math>, es el coeficiente que precede al tiempo en el argumento del coseno | ||
| + | |||
| + | <center><math>\omega = 126\,\frac{\mathrm{rad}}{\mathrm{s}}</math></center> | ||
| + | |||
===Periodo=== | ===Periodo=== | ||
===Número de onda=== | ===Número de onda=== | ||
Revisión de 17:00 23 feb 2009
Contenido |
1 Enunciado
Una perturbación a lo largo de una cuerda se describe mediante la ecuación
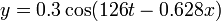
con x e y medidos en centímetros y t en segundos.
Para esta onda, halle su amplitud, frecuencia angular, periodo, número de onda y longitud de onda.
2 Solución
Esta función es una onda viajera correspondiente a la la forma general
que, por se de la forma f(x − vt) es claramente una solución de la ecuación de onda.
2.1 Amplitud
La amplitud de esta onda, A, es el coeficiente que multiplica al coseno. En nuestro caso
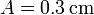
2.2 Frecuencia angular
La frecuencia angular, ω, es el coeficiente que precede al tiempo en el argumento del coseno