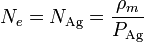Velocidad de arrastre en un hilo
De Laplace
(Nueva página: ==Enunciado== Halle la velocidad de arrastre de los electrones en un cable de plata de 0.5 mm² de sección por el cual circula una corriente de 100 mA. ==Solución...) |
(→Solución) |
||
| Línea 3: | Línea 3: | ||
==Solución== | ==Solución== | ||
| + | La densidad de corriente en el hilo, si se distribuye uniformemente por sus sección será igual a | ||
| + | |||
| + | <center><math>J = \frac{I}{S}=2\times 10^{5}\,\frac{\mathrm{A}}{\mathrm{m}^2}</math></center> | ||
| + | |||
| + | En un hilo metálico los únicos portadores de corriente son los electrones. Por ello, la densidad de corriente será igual a la densidad de carga de estos portadores multiplicada por su velocidad en la dirección de la corriente | ||
| + | |||
| + | <center><math>\mathbf{J} = \sum_k N_k Z_k e \mathbf{v}_k = -N_e e\mathbf{v}_e</math>{{tose}} <math>J = N_e e v_e\,</math></center> | ||
| + | |||
| + | Cada átomo de plata contribuye con un electrón a la corriente. Por ello, el número de electrones de conducción por unidad de volumen coincide con el número de átomos de plata por unidad de volumen. | ||
| + | |||
| + | A su vez, podemos calcular la densidad numérica de átomos conociendo la masa atómica y la densidad de masa, ya que ésta será igual al número de átomos multiplicada por la masa de cada uno | ||
| + | |||
| + | <center><math>\rho_m = P_\mathrm{Ag} N_\mathrm{Ag}\,</math>{{tose}}<math> N_e = N_\mathrm{Ag} = \frac{\rho_m}{P_\mathrm{Ag}}</math></center> | ||
| + | |||
[[Categoría:Problemas de corriente eléctrica]] | [[Categoría:Problemas de corriente eléctrica]] | ||
Revisión de 13:20 23 feb 2009
1 Enunciado
Halle la velocidad de arrastre de los electrones en un cable de plata de 0.5 mm² de sección por el cual circula una corriente de 100 mA.
2 Solución
La densidad de corriente en el hilo, si se distribuye uniformemente por sus sección será igual a
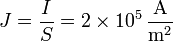
En un hilo metálico los únicos portadores de corriente son los electrones. Por ello, la densidad de corriente será igual a la densidad de carga de estos portadores multiplicada por su velocidad en la dirección de la corriente
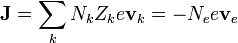


Cada átomo de plata contribuye con un electrón a la corriente. Por ello, el número de electrones de conducción por unidad de volumen coincide con el número de átomos de plata por unidad de volumen.
A su vez, podemos calcular la densidad numérica de átomos conociendo la masa atómica y la densidad de masa, ya que ésta será igual al número de átomos multiplicada por la masa de cada uno