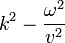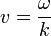Solución de onda estacionaria
De Laplace
(Diferencias entre revisiones)
(Nueva página: ==Enunciado== Una perturbación de una cuerda es de la forma <center><math>y =0.2\cos(126t)\,\mathrm{sen}\,(0.314x)</math></center> con ''x'' e ''y'' medidos en centímetros y ''t'...) |
|||
| Línea 9: | Línea 9: | ||
==Solución== | ==Solución== | ||
| + | [[Imagen:Estacio1.gif|left]] Hay que señalar que la forma de esta solución no es una señal que viaje ni hacia la derecha ni hacia la izquierda. | ||
| + | Comenzamos escribiendo esta solución en la forma más general | ||
| + | |||
| + | <center><math>y =A\cos(\omega t)\,\mathrm{sen}\,(k x)</math>{{qquad}}<math>A=0.2\,\mathrm{cm}</math>{{qquad}}<math>\omega=126\,\mathrm{s}^{-1}</math>{{qquad}}<math>k=0.314\,\mathrm{cm}^{-1}</math></center> | ||
| + | |||
| + | Se trata de demostrar que esta solución cumple una ecuación de la forma | ||
| + | |||
| + | <center><math>\frac{\partial^2 y}{\partial x^2}-\frac{1}{v^2}\,\frac{\partial^2 y}{\partial t^2}=0</math></center> | ||
| + | |||
| + | con <math>v</math> una constante que debemos calcular. | ||
| + | |||
| + | Hallamos las dos derivadas parciales segundas. Respecto al tiempo | ||
| + | |||
| + | <center><math>\frac{\partial y}{\partial t}= -A\omega \,\mathrm{sen}\,(\omega t)\,\mathrm{sen}\,(k x)</math>{{qquad}}<math>\frac{\partial^2y}{\partial t^2}=-A\omega^2\cos(\omega t)\,\mathrm{sen}\,(k x) = -\omega^2 y</math></center> | ||
| + | |||
| + | Respecto a la posición | ||
| + | |||
| + | <center><math>\frac{\partial y}{\partial x}= -Ak\cos(\omega t)\cos(k x)</math>{{qquad}}<math>\frac{\partial^2y}{\partial x^2}=-Ak^2\cos(\omega t)\,\mathrm{sen}\,(k x) = -k^2 y</math></center> | ||
| + | |||
| + | Sustituyendo en la ecuación de onda | ||
| + | |||
| + | <center><math>\frac{\partial^2 y}{\partial x^2}-\frac{1}{v^2}\,\frac{\partial^2 y}{\partial t^2} = -k^2y+\frac{\omega^2}{v^2}y=-\left(k^2-\frac{\omega^2}{v^2}\right)y</math></center> | ||
| + | |||
| + | Esta expresión se anula en todo instante y para todos los puntos si | ||
| + | |||
| + | <center><math>k^2-\frac{\omega^2}{v^2}</math>{{tose}} <math>v = \frac{\omega}{k}</math></center> | ||
[[Categoría:Problemas de movimiento ondulatorio]] | [[Categoría:Problemas de movimiento ondulatorio]] | ||
Revisión de 08:48 22 feb 2009
1 Enunciado
Una perturbación de una cuerda es de la forma
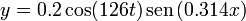
con x e y medidos en centímetros y t en segundos. Demuestre que esta función verifica la ecuación de ondas. ¿Qué velocidad le corresponde?
2 Solución
Comenzamos escribiendo esta solución en la forma más general
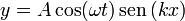
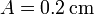
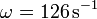
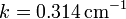
Se trata de demostrar que esta solución cumple una ecuación de la forma
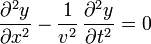
con v una constante que debemos calcular.
Hallamos las dos derivadas parciales segundas. Respecto al tiempo
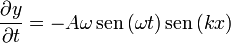
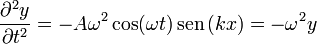
Respecto a la posición
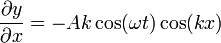
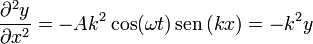
Sustituyendo en la ecuación de onda
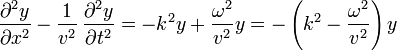
Esta expresión se anula en todo instante y para todos los puntos si
