Percusión sobre una barra. Estudio analítico

De Laplace

(Diferencias entre revisiones)

Revisión de 15:03 11 feb 2018

Contenido

1 Enunciado
2 Barra libre
3 Barra articulada
4 Barra empotrada

1 Enunciado

Suponga una barra homogénea, de masa $m$ y longitud $b$ , situada horizontalmente sobre un plano sin rozamiento.

Estando la barra en reposo, se efectúa sobre ella una percusión 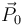$\vec{P}_0$ perpendicular a la dirección de la barra y a una distancia c de su centro.

Empleando las técnicas de la mecánica analítica, determine la velocidad del centro de la barra y la velocidad angular de ésta, así como las posibles fuerzas y momentos impulsivos de reacción, en los casos siguientes:

La barra puede moverse libremente por el plano.
La barra se halla articulada por un extremo O a una pared inmóvil.
La barra se halla empotrada por su extremo O a una pared inmóvil.

2 Barra libre

La ecuación básica que gobierna un sistema sometida a percusiones es la de Lagrange

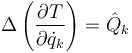
$\Delta\left(\frac{\partial T}{\partial \dot{q}_k}\right)=\hat{Q}_k$

suponiendo coordenadas independientes y siendo 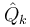$\hat{Q}_k$ la percusión generalizada

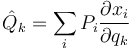
$\hat{Q}_k=\sum_i P_i \frac{\partial x_i}{\partial q_k}$

En nuestro caso el sistema tiene tres grados de libertad, que podemos parametrizar con las dos coordenadas cartesianas del CM y el ángulo θ que la barra forma con OX. Tomamos los ejes de manera que la barra se encuentra inicialmente sobre el eje OX con un extremo en el origen. En este sistema la percusión se aplica en

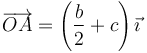
$\overrightarrow{OA}=\left(\frac{b}{2}+c\right)\vec{\imath}$

y tiene el valor

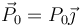
$\vec{P}_0=P_0\vec{\jmath}$

La energía cinética de la barra, en función de estas coordenadas queda

$T=\frac{m}{2}(\dot{x}_G^2+\dot{y}_G^2)+\frac{1}{24}mb^2\dot{\theta}^2$

Aplicando la ecuación de Lagrange a cada coordenada obtenemos las componentes de la velocidad del CM y la velocidad angular.

2.1 Coordenada x

El primer miembro de la ecuación nos da

No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \Delta\left(\frac{\partial T}{\partial \dot{x}_G\right)=m(\dot{x}_G^+-\overbrace{\dot{x}_G^-}^{=0})=m\dot{x}_G^+

Para el segundo miembro, si A es el punto donde se aplica la percusión, queda

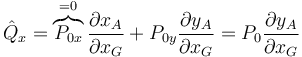
$\hat{Q}_x=\overbrace{P_{0x}}^{=0}\frac{\partial x_A}{\partial x_G}+P_{0y}\frac{\partial y_A}{\partial x_G}=P_0\frac{\partial y_A}{\partial x_G}$

Para obtener esta derivada parcial debemos relacionar la posición del punto A con la de G. En general esta relación es

$x_A=x_G+c\cos(\theta)\qquad\qquad y_A=y_G+c\,\mathrm{sen}(\theta)$

de donde

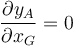
$\frac{\partial y_A}{\partial x_G}=0$

es decir, que mover la barra a derecha o izquierda (variar $x G$ ) no cambia la posición vertical del punto A.

Alternativamente puede emplearse la relación entre velocidades, ya que

$\frac{\partial y_A}{\partial x_G}=\frac{\partial \dot{y}_A}{\partial \dot{x}_G}$

Por la expresión del campo de velocidades

$\vec{v}_A=\vec{v}_G+\vec{\omega}\times\overrightarrow{GA}=(\dot{x}_G\vec{\imath}+\dot{y}_G\vec{\jmath})+\dot{\theta}\vec{k}\times(c\vec{\imath})$

lo que da las relaciones

$\left\{\begin{array}{rcl}\dot{x}_A&=&\dot{x}_G \\ \dot{y}_A&=&\dot{y}_G+c\dot{\theta}\end{array}\right.$

Obtenemos igualmente

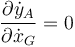
$\frac{\partial \dot{y}_A}{\partial \dot{x}_G}=0$

Aunque el uso de las velocidades parece más complicado, tiene la ventaja de que solo hay que emplear la posición instantánea y no una posición general de la barra.

Por tanto, el CM de la barra no adquiere velocidad en la dirección x

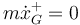
$m\dot{x}_G^+=0$

2.2 Coordenada y

Operamos igualmente y obtenemos

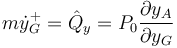
$m\dot{y}_G^+=\hat{Q}_y=P_0\frac{\partial y_A}{\partial y_G}$

Esta derivada ya no es nula

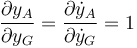
$\frac{\partial y_A}{\partial y_G}=\frac{\partial \dot{y}_A}{\partial \dot{y}_G}=1$

lo que nos da la componente y de la velocidad del CM

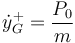
$\dot{y}_G^+ = \frac{P_0}{m}$

A este mismo resultado se llega por aplicación del teorema de la cantidad de movimiento en mecánica vectorial.

2.3 Coordenada theta

Operamos igualmente y obtenemos

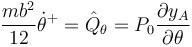
$\frac{mb^2}{12}\dot{\theta}^+=\hat{Q}_\theta=P_0\frac{\partial y_A}{\partial \theta}$

Esta derivada tampoco es nula. Aquí ya hay una ventaja en emplear la relación entre velocidades, ya que permite evitar los senos y cosenos

$\frac{\partial y_A}{\partial \theta}=\frac{\partial \dot{y}_A}{\partial \dot{\theta}}=c$

lo que nos da

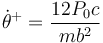
$\dot{\theta}^+ = \frac{12P_0c}{mb^2}$

A este mismo resultado se llega por aplicación del teorema del momento cinético.

En forma vectorial, la velocidad del CM y la angular justo tras la percusión valen

$\vec{v}_G^+ = \frac{P_0}{m}\vec{\jmath}\qquad\qquad \vec{\omega}=\frac{12P_0c}{mb^2}$

El centro de percusiones (centro instantáneo de rotación justo tras la percusión, esto es, el punto alrededor del que empieza a girar) se halla en

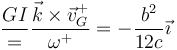
$\frac{GI}=\frac{\vec{k}\times \vec{v}^+_G}{\omega^+}= -\frac{b^2}{12c}\vec{\imath}$

Si $c = b / 6$ , este CIR se halla en el extremo O de la barra.

3 Barra articulada

4 Barra empotrada

@@ Línea 12: / Línea 12: @@
 La ecuación básica que gobierna un sistema sometida a percusiones es la de Lagrange
-<center><math>\Delta\left(\frac{\partial T}{\partial \dot{q}_k\right)=\hat{Q}_k</math></center>
+<center><math>\Delta\left(\frac{\partial T}{\partial \dot{q}_k}\right)=\hat{Q}_k</math></center>
 suponiendo coordenadas independientes y siendo <math>\hat{Q}_k</math> la percusión generalizada
@@ Línea 111: / Línea 111: @@
 Si <math>c = b/6</math>, este CIR se halla en el extremo O de la barra.
 ==Barra articulada==
 ==Barra empotrada==
 [[Categoría:Problemas de mecánica analítica (CMR)]]

Percusión sobre una barra. Estudio analítico

De Laplace

Revisión de 15:03 11 feb 2018

Contenido

1 Enunciado

2 Barra libre

2.1 Coordenada x

2.2 Coordenada y

2.3 Coordenada theta

3 Barra articulada

4 Barra empotrada

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES