Barra apoyada en bloque
De Laplace
(Diferencias entre revisiones)
(→Enunciado) |
|||
| Línea 11: | Línea 11: | ||
==Fuerzas sobre la barra== | ==Fuerzas sobre la barra== | ||
| + | La fuerza en O tiene dos componentes independientes, pero la de A, donde no hay rozamiento, es ortogonal a la barra | ||
| + | |||
| + | <math>\vec{F}_O=F_{Ox}\vec{\imath}+F_{Oy}\vec{\jmath}\qquad\qquad \vec{F}_A=F_A\left(-0.6\vec{\imath}+0.80\vec{\jmath}\right)</math> | ||
| + | |||
| + | Por estar en equilibrio, la suma de fuerzas es nula | ||
| + | |||
| + | <center><math>F_{Ox}-0.60F_A = 0 \qquad\qquad F_{Oy}+0.80F_A-10 = 0</math></center> | ||
| + | |||
| + | y suma de momentos igual a cero | ||
| + | |||
| + | <center><math>\vec{M}_O = (-x_g (mg)+F_A |\overrightarrow{OA})}\vec{k}=(-6.0+F_A)\vec{k}\qquad\Rightarrow\qquad F_A=6.0\,\mathrm{N}</math></center> | ||
| + | y de aquí | ||
| + | |||
| + | <center><math>F_{Ox}=-F_{Ax}=+0.60F_A=3.6\,\mathrm{N}\qquad\qquad F_{Oy}=-0.80 F_A+10=5.2\,\mathrm{N}</math></center> | ||
| + | |||
| + | En forma vectorial | ||
| + | |||
| + | <center><math>\vec{F}_O=(3.6\vec{\imath}+5.2\vec{\jmath})\,\mathrm{N}\qquad\qquad \vec{F}_A=\left(-3.6\vec{\imath}+4.8\vec{\jmath}\right)\,\mathrm{N}</math></center> | ||
==Fuerza sobre el bloque== | ==Fuerza sobre el bloque== | ||
==Coeficiente de rozamiento== | ==Coeficiente de rozamiento== | ||
==Momento de las fuerzas de reacción== | ==Momento de las fuerzas de reacción== | ||
[[Categoría:Problemas de dinámica del sólido rígido (GIE)]] | [[Categoría:Problemas de dinámica del sólido rígido (GIE)]] | ||
Revisión de 16:33 1 feb 2018
Contenido |
1 Enunciado
Una barra homogénea de 10 N de peso y 150 cm de longitud está articulada por uno de sus extremos, O. La barra está apoyada sin rozamiento sobre un bloque cuadrado homogéneo de h = 60cm de lado y 9.6 N de peso fijado al suelo, de manera que su borde está a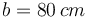 
de O. Sea A el punto del bloque donde se apoya la barra.
- Determine la fuerza que se ejerce sobre la barra en O y en A.
Suponga ahora que el bloque no está soldado al suelo, sino solo apoyado en él, y es mantenido en su posición por la fuerza de rozamiento estático.
- Calcule la resultante de las fuerzas de reacción que el suelo ejerce sobre el bloque.
- Determine el valor mínimo del coeficiente de rozamiento μ para que el sistema se quede en equilibrio.
- Halle el momento resultante de las fuerzas de reacción del suelo sobre el bloque respecto a la esquina B de éste.
2 Fuerzas sobre la barra
La fuerza en O tiene dos componentes independientes, pero la de A, donde no hay rozamiento, es ortogonal a la barra
Por estar en equilibrio, la suma de fuerzas es nula
y suma de momentos igual a cero
y de aquí
En forma vectorial
