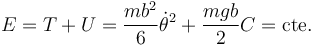Estudio analítico de una barra apoyada
De Laplace
(→Enunciado) |
|||
| Línea 11: | Línea 11: | ||
==Lagrangiana del sistema== | ==Lagrangiana del sistema== | ||
| + | ===Energía cinética=== | ||
| + | Podemos hallar la energía cinética a partir de la expresión general para un sólido | ||
| + | |||
| + | <center><math>T=\frac{1}{2}m|\vec{v}_G|^2+\frac{1}{2}\vec{\omega}\cdot\bar{\bar{I}}\cdot\vec{\omega}</math></center> | ||
| + | |||
| + | En el caso de un movimiento plano esta expresión se reduce a | ||
| + | |||
| + | <center><math>T=\frac{1}{2}n(\dot{x}_G^2+\dot{y}_G^2)+\frac{1}{2}I_{zz}\omega^2</math></center> | ||
| + | |||
| + | La posición del CM es, en función de θ | ||
| + | |||
| + | <center><math>x_G=\frac{b}{2}\mathrm{sen}(\theta)=\frac{b}{2}S\qquad\qquad y_G=\frac{b}{2}\mathrm{cos}(\theta)=\frac{b}{2}C</math></center> | ||
| + | |||
| + | y su velocidad | ||
| + | |||
| + | <center><math>\dot{x}_G=\frac{b}{2}\dot{\theta}C\qquad\qquad \dot{y}_G=-\frac{b}{2}\dot{\theta}S</math></center> | ||
| + | |||
| + | Esto nos da la energía cinética | ||
| + | |||
| + | <center><math>T=\frac{1}{2}\left(\frac{b^2}{4}\dot{\theta}^2\right)+\frac{1}{2}\left(\frac{1}{12}mb^2\right)\dot{\theta}^2=\frac{mb^2}{6}\dot{\theta}^2</math></center> | ||
| + | |||
| + | También podemos llegar a este resultado empleando la expresión para una barra conocidas las velocidades de sus extremos A y B | ||
| + | |||
| + | <center><math>T=\frac{m}{6}(|\vec{v}_A|^2 +|\vec{v}_B|^2+\vec{v}_A\cdot\vec{v}_B)</math></center> | ||
| + | |||
| + | ===Energía potencial=== | ||
| + | La energía potencial gravitatoria la da la altura del CM | ||
| + | |||
| + | <center><math>U=mgy_G=\frac{mgb}{2}C</math></center> | ||
| + | |||
| + | ===Lagrangiana=== | ||
| + | Restamos las dos cantidades | ||
| + | |||
| + | <center><math>\mathcal{L}=T-U=\frac{mb^2}{6}\dot{\theta}^2-\frac{mgb}{2}C</math></center> | ||
| + | |||
==Ecuación de movimiento== | ==Ecuación de movimiento== | ||
| + | Aplicamos la ecuación de Lagrange a la coordenada θ | ||
| + | |||
| + | <center><math>\frac{\partial\mathcal{L}}{\partial\dot{\theta}}=\frac{mb^2}{3}\dot{\theta}\qquad\qquad \frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial\mathcal{L}}{\partial\dot{\theta}}\right)=\frac{mb^2}{3}\ddot{\theta}</math></center> | ||
| + | |||
| + | Por otro lado | ||
| + | <center><math>\frac{\partial\mathcal{L}}{\partial{\theta}}=\frac{mgb}{2}S</math></center> | ||
| + | |||
| + | lo que nos da la ecuación de movimiento | ||
| + | |||
| + | <center><math>\frac{mb^2}{3}\ddot{\theta}-\frac{mgb}{2}S=0\qquad\Rightarrow\qquad \ddot{\theta}=\frac{3g}{2b}\mathrm{sen}(\theta)</math></center> | ||
| + | |||
| + | Vemos que empleando la mecánica analítica llegamos al resultado de forma mucho más corta que mediante mecánica vectorial, ya que no precisamos considerar la acción de las fuerzas de reacción. | ||
| + | |||
==Constante de movimiento== | ==Constante de movimiento== | ||
| + | La lagrangiana de este problema no depende del tiempo y la energía cinética es una función cuadrática de la velocidad generalizada. Por tanto se conserva la energía mecánica | ||
| + | |||
| + | <center><math>E=T+U=\frac{mb^2}{6}\dot{\theta}^2+\frac{mgb}{2}C=\mathrm{cte.}</math></center> | ||
==Fuerza de reacción== | ==Fuerza de reacción== | ||
==Separación de la pared== | ==Separación de la pared== | ||
==Movimiento tras la separación== | ==Movimiento tras la separación== | ||
[[Categoría:Problemas de mecánica analítica (CMR)]] | [[Categoría:Problemas de mecánica analítica (CMR)]] | ||
Revisión de 20:22 20 ene 2018
Contenido |
1 Enunciado
Supongamos que tenemos una barra de masa m y longitud b apoyada en el suelo y en una pared vertical, sometida a la acción del peso (vertical y hacia abajo) y a las fuerzas de reacción en los puntos de contacto. No hay rozamiento con las superficies

- Determine la lagrangiana del sistema.
- Halle la ecuación de movimiento para el ángulo θ.
- Determine una constante de movimiento no trivial.
- Añadiendo una coordenada x que representaría la separación de la barra respecto de la pared vertical, calcule la fuerza de reacción ejercida por la pared.
- Existe un valor de θ para el cual la barra se separa de la pared. Determine este valor.
- Halle la ecuación de movimiento para la barra una vez que se ha separado de la pared.
2 Lagrangiana del sistema
2.1 Energía cinética
Podemos hallar la energía cinética a partir de la expresión general para un sólido
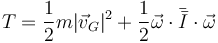
En el caso de un movimiento plano esta expresión se reduce a
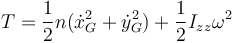
La posición del CM es, en función de θ

y su velocidad

Esto nos da la energía cinética
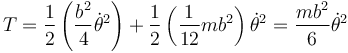
También podemos llegar a este resultado empleando la expresión para una barra conocidas las velocidades de sus extremos A y B
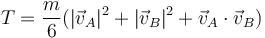
2.2 Energía potencial
La energía potencial gravitatoria la da la altura del CM
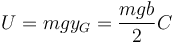
2.3 Lagrangiana
Restamos las dos cantidades
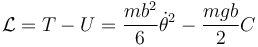
3 Ecuación de movimiento
Aplicamos la ecuación de Lagrange a la coordenada θ
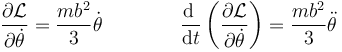
Por otro lado
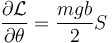
lo que nos da la ecuación de movimiento
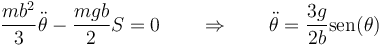
Vemos que empleando la mecánica analítica llegamos al resultado de forma mucho más corta que mediante mecánica vectorial, ya que no precisamos considerar la acción de las fuerzas de reacción.
4 Constante de movimiento
La lagrangiana de este problema no depende del tiempo y la energía cinética es una función cuadrática de la velocidad generalizada. Por tanto se conserva la energía mecánica