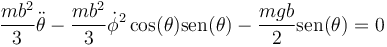Péndulo compuesto. Análisis por mecánica analítica (CMR)
De Laplace
(Página creada con '==Enunciado== Para el sistema del problema “Péndulo compuesto” analice el problema general mediante las técnicas de mecánica analíti…') |
|||
| Línea 10: | Línea 10: | ||
==Lagrangiana del sistema== | ==Lagrangiana del sistema== | ||
| + | En este sistema no hay fuerzas no conservativas y los vínculos son geométricos (ya que el único vínculo es que el extremo O es un punto fijo). Por ello, las ecuaciones de movimiento pueden obtenerse a partir de las ecuaciones de Lagrange | ||
| + | |||
| + | <center><math>\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial\mathcal{L}}{\partial\dot{q}_k\right)-\frac{\partial\mathcal{L}}{\partial q_k}=0</math></center> | ||
| + | |||
| + | siendo | ||
| + | |||
| + | <center><math>\mathcal{L}=T-U</math></center> | ||
| + | |||
| + | la lagrangiana del sistema. Aquí <math>T=K</math> es la energía cinética y U la potencial. | ||
| + | |||
| + | La energía cinética de un sólido con un punto fijo O se puede calcular como | ||
| + | |||
| + | <center><math>T=\frac{1}{2}\vec{\omega}\cdot\vec{L}_O=\frac{1}{2}\vec{\omega}\cdot\bar{\bar{I}}\cdot\vec{\omega}</math></center> | ||
| + | |||
| + | Tal como se ve en el problema citado, la expresión más simple de la energía cinética se obtiene en un sistema de referencia ligado en el que el eje <math>OZ_2</math> va en la dirección de la barra y los otros dos son ortogonales a éste por O. En este sistema la energía cinética tiene la expresión | ||
| + | |||
| + | <center><math>T=\frac{mb^2}{2}(\omega_X^2+\omega_Y^2)</math></center> | ||
| + | |||
| + | A su vez, como se ve en el mismo problema, las componentes de la velocidad angular en el sistema ligado se relacionan con las derivadas de los ángulos por | ||
| + | |||
| + | <center><math>\omega_X=\dot{\theta}\qquad\qquad\Omega_Y=\dot{\phi}\,\mathrm{sen}(\theta)=\dot{\phi}S</math></center> | ||
| + | |||
| + | lo que nos da la expresión para la energía cinética | ||
| + | |||
| + | <center><math>T=\frac{mb^2}{6}(\dot{\theta}^2+\dot{\phi}^2\mathrm{sen}^2(\theta))</math></center> | ||
| + | |||
| + | Por su parte, la energía potencial sale de la altura del CM | ||
| + | |||
| + | <center><math>U=mgh_G=-mg\frac{b}{2}\cos(\theta)</math></center> | ||
| + | |||
| + | Por tanto la lagrangiana del sistema es | ||
| + | |||
| + | <center><math>\mathcal{L}=\frac{mb^2}{6}(\dot{\theta}^2+\dot{\phi}^2\mathrm{sen}^2(\theta))+mg\frac{b}{2}\cos(\theta)</math></center> | ||
==Ecuaciones de movimiento== | ==Ecuaciones de movimiento== | ||
| + | ===Para el ángulo ϕ=== | ||
| + | La ecuación de Lagrange para este ángulo es | ||
| + | |||
| + | <center><math>\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial\mathcal{L}}{\partial\dot{\phi}}\right)-\frac{\partial\mathcal{L}}{\partial \phi}=0</math></center> | ||
| + | |||
| + | Calculamos en primer lugar el momento conjugado | ||
| + | |||
| + | <center><math>p_\phi=\frac{\partial\mathcal{L}}{\partial\dot{\phi}}=\frac{mb^2}{3}\dot{\phi}\mathrm{sen}^2(\theta)</math></center> | ||
| + | |||
| + | siendo su derivada temporal | ||
| + | |||
| + | <center><math>\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial\mathcal{L}}{\partial\dot{\phi}}\right)=\frac{mb^2}{3}(\ddot{\phi}\mathrm{sen}^2(\theta)+2\dot{\phi}\dot{\theta}\cos(\theta)\mathrm{sen}(\theta))</math></center> | ||
| + | |||
| + | Por otro lado, la lagrangiana no depende explícitamente del ángulo ϕ | ||
| + | |||
| + | <center><math>\frac{\partial\mathcal{L}}{\partial \phi}=0</math></center> | ||
| + | |||
| + | por lo que la ecuación de movimiento buscada es | ||
| + | |||
| + | <center><math>\frac{mb^2}{3}(\ddot{\phi}\mathrm{sen}^2(\theta)+2\dot{\phi}\dot{\theta}\cos(\theta)\mathrm{sen}(\theta))=0</math></center> | ||
| + | |||
| + | Podemos sacar factores comunes y reducirla a | ||
| + | |||
| + | <center><math>\ddot{\phi}S+2\dot{\phi}\dot{\theta}C=0</math></center> | ||
| + | |||
| + | ===Para el ángulo θ== | ||
| + | De manera análoga operamos con el otro ángulo. Su momento conjugado vale | ||
| + | |||
| + | <center><math>p_\theta=\frac{\partial\mathcal{L}}{\partial\dot{\theta}}=\frac{mb^2}{3}\dot{\theta}</math></center> | ||
| + | |||
| + | cuya derivada respecto al tiempo es simplemente | ||
| + | |||
| + | <center><math>\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{\partial\mathcal{L}}{\partial\dot{\phi}}\right)=\frac{mb^2}{3}\ddot{\theta}</math></center> | ||
| + | |||
| + | En cuanto a la derivada respecto al ángulo tenemos términos en la energía cinética y en la potencial | ||
| + | |||
| + | <center><math>\frac{\partial\mathcal{L}}{\partial \theta}=\frac{mb^2}{3}\dot{\phi}^2\cos(\theta)\mathrm{sen}(\theta)+\frac{mgb}{2}\mathrm{sen}(\theta) </math></center> | ||
| + | |||
| + | lo que nos da la ecuación de movimiento | ||
| + | |||
| + | <center><math>\frac{mb^2}{3}\ddot{\theta}-\frac{mb^2}{3}\dot{\phi}^2\cos(\theta)\mathrm{sen}(\theta)-\frac{mgb}{2}\mathrm{sen}(\theta)=0</math></center> | ||
==Constantes de movimiento== | ==Constantes de movimiento== | ||
==Ecuación para θ== | ==Ecuación para θ== | ||
==Movimiento con inclinación constante== | ==Movimiento con inclinación constante== | ||
[[Categoría:Problemas de mecánica analítica (CMR)]] | [[Categoría:Problemas de mecánica analítica (CMR)]] | ||
Revisión de 22:34 9 ene 2018
Contenido |
1 Enunciado
Para el sistema del problema “Péndulo compuesto” analice el problema general mediante las técnicas de mecánica analítica. Se tiene una barra homogénea de longitud b y masa m, articulada mediante una rótula en un extremo O y sometida a la acción de la gravedad. La barra puede tanto variar su ángulo θ con la vertical como el ángulo ϕ alrededor de OZ.
Para este sistema
- Calcule la lagrangiana del sistema.
- Halle las ecuaciones de movimiento para los dos ángulos de giro, θ y ϕ
- Obtenga dos constantes de movimiento no triviales.
- Con ayuda de las constantes de movimiento, halle una ecuación que incluya solamente a θ
- Calcule el valor que debe tener la velocidad angular
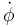 si se desea que la barra mantenga una inclinación constante respecto a la vertical.
si se desea que la barra mantenga una inclinación constante respecto a la vertical.
2 Lagrangiana del sistema
En este sistema no hay fuerzas no conservativas y los vínculos son geométricos (ya que el único vínculo es que el extremo O es un punto fijo). Por ello, las ecuaciones de movimiento pueden obtenerse a partir de las ecuaciones de Lagrange
siendo
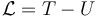
la lagrangiana del sistema. Aquí T = K es la energía cinética y U la potencial.
La energía cinética de un sólido con un punto fijo O se puede calcular como
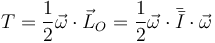
Tal como se ve en el problema citado, la expresión más simple de la energía cinética se obtiene en un sistema de referencia ligado en el que el eje OZ2 va en la dirección de la barra y los otros dos son ortogonales a éste por O. En este sistema la energía cinética tiene la expresión
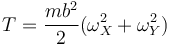
A su vez, como se ve en el mismo problema, las componentes de la velocidad angular en el sistema ligado se relacionan con las derivadas de los ángulos por
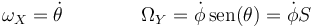
lo que nos da la expresión para la energía cinética
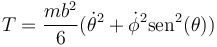
Por su parte, la energía potencial sale de la altura del CM
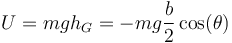
Por tanto la lagrangiana del sistema es
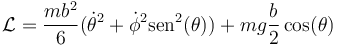
3 Ecuaciones de movimiento
3.1 Para el ángulo ϕ
La ecuación de Lagrange para este ángulo es
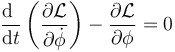
Calculamos en primer lugar el momento conjugado
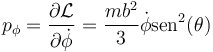
siendo su derivada temporal
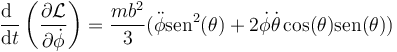
Por otro lado, la lagrangiana no depende explícitamente del ángulo ϕ
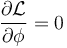
por lo que la ecuación de movimiento buscada es
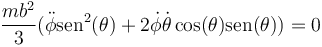
Podemos sacar factores comunes y reducirla a
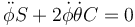
4 =Para el ángulo θ
De manera análoga operamos con el otro ángulo. Su momento conjugado vale
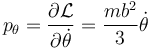
cuya derivada respecto al tiempo es simplemente
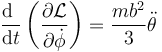
En cuanto a la derivada respecto al ángulo tenemos términos en la energía cinética y en la potencial

lo que nos da la ecuación de movimiento